高周波の非線形特性を高精度に解析、新概念の「Xパラメータ」で実現:無線通信技術(2/5 ページ)
米Agilent Technologies(アジレント・テクノロジー)社は、高周波回路の非線形特性を高い精度でコンピュータ解析(シミュレーション)するための基本技術を開発した。無線システムの高度化などを背景に、高周波回路のシミュレーションにおける非線形特性の解析精度を高めたいという需要が高まっており、これに対応する。
無線技術の普及がすさまじい勢いで進んでいる。われわれは今や、無線技術に囲まれて暮らしているといっても過言ではない。携帯電話機はもとより、パソコンやその周辺機器、デジタル家電、自動車に至るまで、身の回りのさまざまな機器に無線通信機能が搭載されている。さらに、ビル管理システムやセンサー・ネットワークといったインフラ・システムにも無線化の動きがある。
こうした無線技術の普及は、消費者にとっては生活の利便性が高まるため、歓迎すべき流れだろう。無線関連の製品を供給するメーカーにとっても、市場機会が増える可能性があり、前向きにとらえられる。ところが、無線技術の普及に伴って、無線回路の開発そのものは難しさを増しており、無線関連の半導体チップや部品、機器を手掛けるメーカーにとって大きな課題になっているという実情もある。
無線回路の開発難易度が高まっている理由としては、無線技術の応用範囲の拡大に伴って新たな通信方式が次々と登場する一方で、無線機能を搭載した最終製品の市場における寿命が短くなったり、価格が低下したりしていることが挙げられる。すなわち無線関連メーカーは、新しい無線通信方式に対応した製品を、これまで以上に短い期間かつ低いコストで開発することを求められているわけだ。しかも、製品の価値を高めて競合他社との差別化を図るため、高い無線特性を低い消費電力で実現することも欠かせない。
こうした課題の解決には、コンピュータ・シミュレーションの活用が必須である。無線回路の振る舞いをシミュレーションによって解析し、その結果を基に無線回路を最適設計すれば、実機の試作回数を大幅に削減可能だ。開発期間の短縮や開発コストの低減につながる。
非線形特性の高精度予測が難しい
ただし、高周波領域の無線信号を扱うコンピュータ・シミュレーションは完全無欠ではない。解析対象の事象によっては、精度が十分に得られない場合がある。そのため無線回路の開発現場では、予測不可能な試作のやり直しが発生したり、目標性能の達成までに要する回路修正の工数見積もりが難しいといった事態が生じている。
無線回路のコンピュータ・シミュレーションにおいて、高精度の予測が特に難しいのは、非線形特性である(図1)。具体的には、主にトランジスタなどの能動素子の非線形動作に起因して生じる、高調波歪みや隣接チャネル漏えい電力といった特性である(4ページ目の別掲記事「電子回路の非線形性」を参照)。
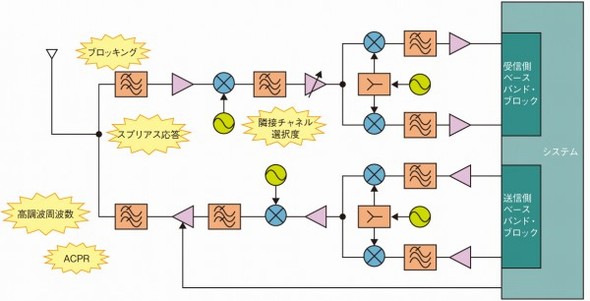
図1 無線回路の非線形性評価 無線回路を開発する際には、通信規格ごとに定められた、非線形特性に関係する仕様値を満たさなければならない。具体的には、高調波周波数やスプリアス応答、隣接チャネル漏えい電力比(ACPR:Adjacent Channel Power Ratio)、相互変調歪み(IMD:Inter Modulation Distortion)などである。
非線形特性の高精度予測が難しい大きな理由はモデルにある。非線形特性を含めて回路を評価する場合、一般的には、ビヘイビア・モデルを使う。ただし、ビヘイビア・モデルにはいくつかの種類があり、それぞれにモデルとしての特性に制約がある。このため選択するモデルによっては、能動素子の振る舞いを十分に表現できない場合がある。例えば、基本波を入力したときに出力側に現れる基本波成分については表現できるが、出力側に実際には現れる高調波成分については表現できないといった制約である。(別掲記事「ビヘイビア・モデルとデバイス・モデル」を参照)。
一方、モデル対象の電気的な物理現象を表現するパラメータを測定して作成するいわゆるデバイス・モデルは、高調波のモデル精度については優れているものの、無線回路の設計者は容易に入手できないというのが実情である。このモデルの作成にはさまざまな測定と、そのデータに基づく高度なモデリング技術が必要で、実際に作成できるのは高周波トランジスタなどを手掛ける半導体ベンダーなど一部に限られているからだ。しかもこうした半導体ベンダーは、デバイス・モデルを介して半導体プロセス技術の知的財産が流出してしまうことを恐れて、デバイス・モデルを社外に提供しないことが多い。
Sパラメータを基に非線形領域に拡張
そこで当社(アジレント・テクノロジー)は、無線回路の設計者が手元で作成できる上、非線形特性を高い精度で表現できるパラメータを提唱する。これを「Xパラメータ」と呼ぶ。小信号(線形)領域の特性を表現するパラメータである「Sパラメータ」を基に、非線形領域の動作を表現できるように拡張を施した。Sパラメータと同様に、モデル対象の高周波素子をベクトル・ネットワーク・アナライザをベースとする測定器で実際に測定し、その結果得られたデータを用いて、高周波素子の振る舞いを表現する。
Xパラメータを使えば、コンピュータ・シミュレーション上で無線回路の非線形特性を高い精度で予測できる。従って、各種の無線通信規格に準拠した無線回路を、所定の期間で開発できる可能性が高まる。すでに当社は、Xパラメータの測定機能をオプションで搭載可能なベクトル・ネットワーク・アナライザを製品化済みである。さらに、Xパラメータを使って無線回路の特性をシミュレーションできる環境も用意した。
パワー・アンプの高効率化に効く
例えば、最終段の電力増幅を担うパワー・アンプ回路の開発にXパラメータを適用すれば、高効率化に威力を発揮するだろう。パワー・アンプの高効率化は、電池駆動の携帯型機器における低消費電力化や、大電力を扱う無線基地局の熱設計の容易化などに向けて、現在特に重要度が高まっている。実際に、スイッチング動作を利用して効率を改善するE級/F級のパワー・アンプが増えている。こうしたスイッチング動作のパワー・アンプでは、高調波の振る舞いをうまく制御することが主な課題になるため、高調波の振る舞いを高い精度で予測できるXパラメータが強力な開発ツールになるはずだ。
以下に、Xパラメータについて詳しく解説する。まずXパラメータの概念や実態について説明し、次にベクトル・ネットワーク・アナライザによるXパラメータの作成方法について述べる。最後に、高周波回路シミュレータ上でのXパラメータの活用方法について解説する。
Xパラメータとは
Xパラメータとは、先に述べた通り、線形領域における素子の入出力特性を表現するパラメータであるSパラメータを、非線形領域に拡張したものである。Sパラメータと同様に、測定によって簡単に求められ、高周波回路シミュレータ上で被測定物である素子の周波数領域における振る舞いを表現する。
すなわちXパラメータは、素子に対する入力と出力の関係のみを表現しており、素子の内部構造に関してはブラック・ボックスとして扱う。このため、Sパラメータと同様に、素子をモデル化する際に素子の内部構造に関する知識が不要というメリットがある。5ページ目の別掲記事「ビヘイビア・モデルとデバイス・モデル」で説明しているように、モデリングを本来の業務としないエンジニアにとって、高精度の非線形モデルを入手することは非常に難しい。Xパラメータによるシミュレーションは、これを軽減し得る有力な方法になるだろう。
Sパラメータとの違いは、従来のSパラメータが対応する線形領域に加えて、素子の非線形領域における振る舞いも表現できることだ。つまり、Sパラメータが素子の入出力関係における基本波の情報しか含んでいないのに対し、Xパラメータは高調波の情報も含んでいる。具体的には、素子の非線形性によって生じた高調波と、素子に外部から入力された高調波の相互関係を、振幅と位相の両方について関連付けた情報を備えている。
非線形の挙動をパラメータで表す
それでは具体例を示しながら、Xパラメータが表現する素子の振る舞いについて説明していこう。ここでは、最も簡単な2ポート素子を例に挙げる(図2)。
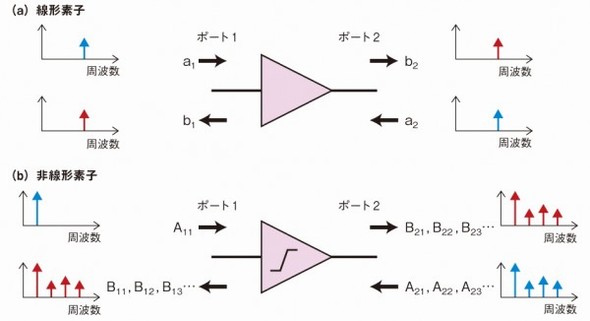
図2 線形素子と非線形素子の振る舞い 2ポート素子を例に、各ポートに入出力する信号のイメージを示した。(a)線形素子では入出力で周波数関係は変わらない。(b)非線形素子では、高調波が発生する上、次数の異なる高調波同士が影響し合う。
線形素子のパラメータ表現では通常、素子への入力信号をa、素子からの出力信号をbと定義し、各信号が複数のポートのいずれに対するものかを識別するために、ポートの番号を添え字とする。例えば、a1はポート1への入力信号を表し、b2はポート2の出力信号を表す。そして、素子に対する入力と出力の関係をa1、a2、b1、b2の比で表現したパラメータがSパラメータである。例えば、S21はポート1の入力信号(a1)とポート2の出力信号(b2)の比(b2/a1)であり、物理的には素子の挿入損失や利得を表す。
非線形素子でも線形素子の場合と同様に、ポート1から入力した信号をA1、ポート2で観測される出力信号をB2といった具合に定義する。線形素子の場合と異なるのは、基本波のみが入力された場合でも、出力側では基本波成分に非線形素子の内部で生成された非線形性分(高調波)が重畳されるという点である。このため、非線形素子の出力は、基本波とその高次高調波が混在する信号になる。
XパラメータもSパラメータと同様に、入力信号と出力信号の関係を表現するパラメータだと先に述べた。しかしXパラメータが対象とする信号は、今説明した通り、基本波と高次高調波が混在する信号である。すなわち、ある周波数の信号は、実際には基本波と高次高調波の両方の成分を合成したものになる。そこでXパラメータでは、非線形領域における素子の振る舞いを正確に表現するため、各周波数における基本波成分と高次高調波成分それぞれの寄与分の情報を取り込む。具体的には、基本波と高次高調波それぞれについて、振幅と位相の関係を把握して、それらをパラメータ表現する。次のページでは、その具体的な方法について解説する。
電子回路の非線形性
ある素子や回路に対して、入力信号と出力信号が比例関係にあるとき、その素子や回路は「線形」であるという。その反対に、線形でない(比例関係が成り立たない)場合は「非線形」であるという(図A-1)。一般に、トランジスタやダイオードなどの半導体能動素子は、非線形性を備えている。
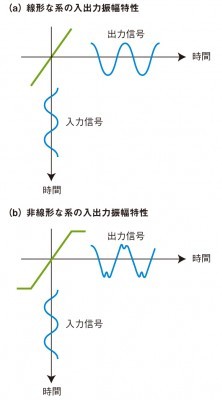
図A-1 時間領域では波形が歪む (a)は線形な素子や回路の入出力波形、(b)は非線形な素子や回路の入出力波形である。線形では入力と出力の波形が相似関係を維持しているのに対し、非線形では出力波形が歪んでいる。
非線形な素子や回路では、入力した波形が歪んで出力される。これを周波数領域で見ると、入力した基本波の高調波が発生していることに等しい(図A-2)。
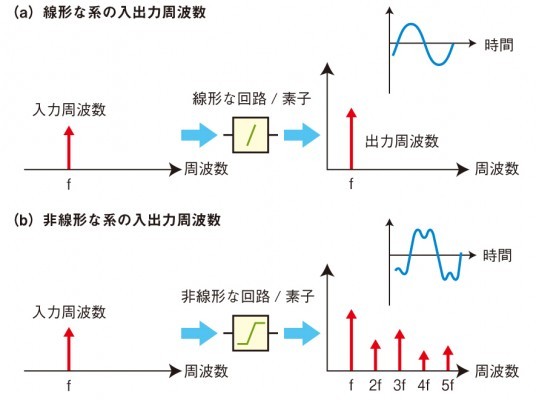
図A-2 周波数領域では高調波が発生 (a)は線形な素子や回路の入出力周波数特性、(b)は非線形な素子や回路の入出力周波数特性である。線形では入力の周波数成分(基本波)がそのまま出力に現れる。振幅や位相は変化しても、周波数は変わらない。これに対し非線形では、基本波に加えて、高調波成分が発生する。これを時間領域で見ると、図A(b)のように入力波形が歪んで出力されている状態である。
こうした非線形性は、線形性を利用する場合は好ましくない特性である。例えば、オーディオ機器のアンプ回路は、入力となる音源信号の波形をなるべく比例関係を保ったまま大きく増幅して出力できることが望ましい。入出力の間に非線形性による歪みが加わると、音源信号の再現性が損なわれてしまう。
ただし、無線送受信回路に使うミキサーや変調器など、非線形性が不可欠な場合もある。例えばミキサーは、非線形歪みによって生じる高調波成分を選択的に取り出すことで、入出力間の周波数変換機能を実現している。
ビヘイビア・モデルとデバイス・モデル
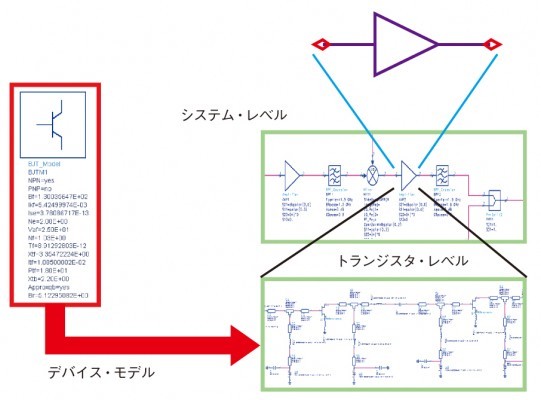
高周波回路シミュレーションで利用するモデルは、大きく「ビヘイビア・モデル」と「デバイス・モデル」の2つに分けられる(図B-1)。いずれのモデルも、シミュレータ上での動作が、モデル化した対象物の実際の振る舞いに近ければ近いほど、回路全体の特性を高い精度で予測できる。
ビヘイビア・モデルは、その名の通り、対象物である素子や回路の振る舞い(ビヘイビア)をモデル化したものだ。「ある信号を入力した際に、対象物がどういった信号を出力するか」という入出力間の関係を数式としてモデル化しており、素子や回路の内部構造については完全にブラック・ボックスとして扱う(図B-2)。
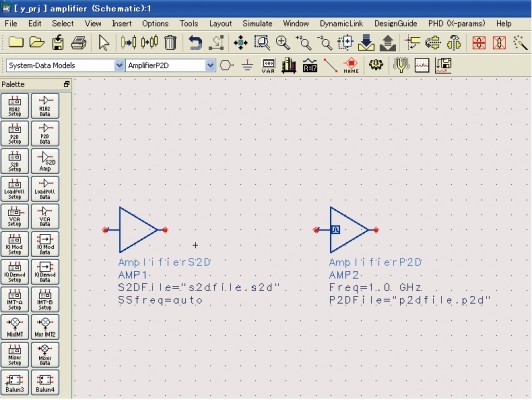
各種モデルのうち、高周波回路の設計開発で最も広く利用されているのがSパラメータである。一般にはベクトル・ネットワーク・アナライザを使って測定する。例えば低雑音アンプ(LNA)を対象物とした測定では、測定者はLNAの内部構造を知る必要はない。ベクトル・ネットワーク・アナライザに接続し、適切なバイアスを与えた状態で測定を実行すれば、Sパラメータが得られる。このデータが、対象物の入出力間の特性を行列式で表した際のパラメータ値になるわけだ。市販の高周波回路シミュレータは、Sパラメータの測定データをそのまま、特定条件におけるビヘイビア・モデルとして扱える。
もう一方のデバイス・モデルは、電子回路を構成する素子(デバイス)を1つ1つモデル化したものである。具体的には、能動素子であるトランジスタやダイオード、受動素子である抵抗やコンデンサ、インダクタなどを個別のモデルとして扱う。
これらのモデルの実体はSpiceモデルであり、作成するには素子の電気的な物理現象を表現する「Spiceパラメータ」と呼ばれるパラメータを、測定によって求める必要がある(図B-3)。例えば能動素子のデバイス・モデルを作成するには、半導体パラメータ測定器によるDC(直流)特性測定、LCRメーターによるC-V(静電容量-電圧)特性測定、ベクトル・ネットワーク・アナライザによるSパラメータ測定が必要で、測定点数によって異なるが一般にかなりの測定時間を費やすことになる。

図B-3 デバイス・モデルの例 BJT(バイポーラ・ジャンクション・トランジスタ)モデルの例である。対象物の測定値を基に、Bf(最大順方向)やIkf(順方向大電流減少点)などのSpiceパラメータの値を設定することでモデル化する。
さらに、Spiceパラメータだけでは対象物の電気的特性を正確に表現できない場合は、等価回路を追加した上で、モデル全体の振る舞いが対象物と同等になるように、等価回路を構成する各素子の定数を調整しなければならない。実際の対象物の動作領域を把握しておくとともに、等価回路の周波数依存性などを十分考慮する必要があり、高度なモデリング技術が求められる。
Copyright © ITmedia, Inc. All Rights Reserved.