第4回 基本現象を応用して回路設計 〜 フィルタ 〜：Analog ABC（アナログ技術基礎講座）

[美齊津摂夫，ディー・クルー・テクノロジーズ]

→「Analog ABC（アナログ技術基礎講座）」連載一覧

　アナログ回路を設計するには、基本的な現象や原則を理解して応用することが大切です。その例として今回は、前回説明した共振現象の応用例として、フィルタ回路を取り上げます。

　フィルタ回路は、インダクタンス（L）、コンデンサ（C）、抵抗素子（R）のいずれかを組み合わせて構成します^＊1）。周波数に対してインピーダンスが変化することを利用して、狙った周波数成分だけを取り出したり、不要な周波数成分を取り除いたりする役割を担っています。前回に紹介したように、LとCを組み合わせると、インピーダンスが極端に大きくなったり、小さくなったりする共振現象が発生します。フィルタ回路にはいくつかのタイプがありますが、共振現象を積極的に活用したタイプもあれば、逆に共振現象を抑えるための対策が必要なタイプもあります。フィルタ回路を設計するには、共振現象とうまく付き合う必要があるのです。

＊1） 実際の電子回路では、表面弾性波（SAW）フィルタや水晶（MCF）フィルタ、誘電体フィルタなどもあります。

周波数で変化する減衰器

　フィルタ回路は、その通過特性に応じて4つのタイプに分けられます。その内訳は、低い周波数成分のみを通過させる低域通過フィルタ（LPF）、高い周波数成分のみを通過させる高域通過フィルタ（HPF）、特定の範囲の周波数成分のみを通過させる帯域通過フィルタ（BPF）、特定の周波数成分のみを通過させない帯域阻止フィルタ（BEF）です。例えば、雑音が多いスイッチング電源回路に、LPFを追加すれば、高い周波数成分（雑音）を取り除けます。また、後段回路に信号のみを伝えて、低い周波数成分であるバイアス電圧変動を伝えないようにするには、HPFを活用します。

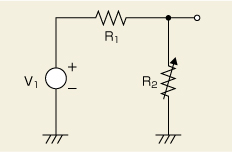
図1　フィルタ回路の構成を単純化　フィルタは周波数によって抵抗値が変わる減衰器です。最も単純な減衰器は抵抗を2つ使った回路で、そのうちR2をC（またはL）に置き換えると1次傾斜（20dB/dec）になります。

　基本的にこれらのフィルタ回路は、周波数によって減衰量が変わる減衰器（アッテネータ）と考えられます。最も単純な減衰器は抵抗素子を2つ使ったものです（図1）。図1に示したR₁とR₂のうち、R₂が小さくなると出力信号は小さくなります（言い換えると、減衰量が増えます）。R₁を大きくしても出力信号が小さくなります。ただし、周波数が変わっても抵抗素子の抵抗値（インピーダンスの大きさ）は変わりません。これに対して、LやCを使えば、周波数に応じて抵抗値（減衰量）を変えられます。例えば、R₁が抵抗素子のままで、R2をCに置き換えれば「ある周波数」を境に、周波数が高くなるにつれて出力信号は小さくなります。一方、R₂をLにすれば、「ある周波数」を境に、周波数が低くなるにつれて出力信号が小さくなります。

　「ある周波数」のことをカットオフ周波数（遮断周波数）と呼びます。カットオフ周波数とは、図1でR₁とR₂の部分の抵抗値が等しくなる周波数です。R2をC（またはL）に変えた場合には、カットオフ周波数を境にして20dB/decの傾き（「1次傾斜」と呼びます）で減衰していきます。dec（ディケイド）とは10倍（または1/10）を意味しますので、周波数が10倍（または1/10）になると、出力信号の大きさが20dB減衰、つまり1/10になることを示しています。周波数という時間軸のパラメータが、「出力信号の大きさ」という時間に関係ないパラメータときれいな相関があることに、自然現象の不思議さを感じます。

　フィルタの減衰量が20dB/decでは足りない場合はどうするのかというと、LとCの両方を使います（図2）。従って、共振現象とうまく付き合う必要が出てきます。

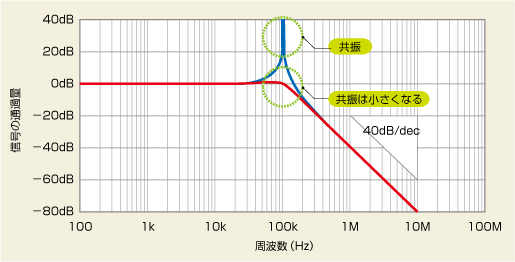
図2　低域通過フィルタの周波数特性　LPFでは、カットオフ周波数を境に信号が減衰していきます。図3に示したフィルタ回路の周波数特性を示しました。図3（a）のダンピング抵抗を挿入しない場合（青線）は、共振現象によって鋭いピーキングが現れます。図3（b）のようにダンピング抵抗を挿入することでピーキングを抑えます（赤線）。

　図3を見て下さい。図3（a）のフィルタ回路では、LとCのインピーダンスが周波数変化に対して同時に変わるので、出力信号を大きく減衰させることができます。具体的には、LとCの両方を使ったときの減衰量は40dB/dec（「2次傾斜」と呼びます）になり、周波数が10倍になったときの出力信号を1/100に減衰させることができます。

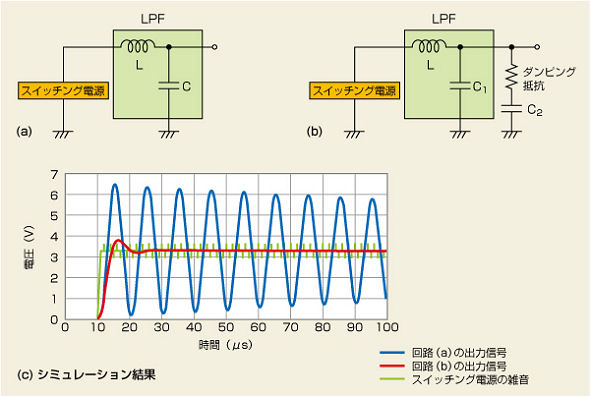
図3　低域通過フィルタの効果　スイッチング電源の雑音をLPFで抑制する場合を想定します（a）。LとCのみでは、共振現象によって出力信号が大きく変動してしまうため、ダンピング抵抗を挿入します（b）。出力信号のシミュレーション結果を見ると、変動が抑えられていることが分かります（c）。

　しかし、良いことばかりではありません。LとCの両方を使ったフィルタ回路では、前述のように共振が発生します。先ほど説明した4つのフィルタ回路のうち、BPFとBEFは、共振現象を積極的に活用してフィルタを実現しています。ところが、LPFやHPFに関しては、共振現象は都合が悪いのです。

　図3（a）では、スイッチング電源が発生した雑音を取り除こうと、LPFを挿入した場合を想定しています。図3（c）はシミュレーション結果です。確かに、スイッチング電源の雑音（緑色）は、LPFの効果で出力信号（青色）に現れていません。ところが、電源の起動とともに出力信号が約0Vから約6.5Vの間を大きく振動してしまいます。電源起動時に共振してしまうのは、LPFの入力信号（電源の出力）がステップ状の波形なので、共振周波数の成分も含まれているからです。このとき、振幅の最大値は定格（3.3V）の2倍近い電圧値に達し、耐圧の低い電子部品の場合、破壊されてしまいます。

　これを防ぐために、LPFのCと並列に、ダンピング抵抗を挿入します（図3（b））。これによって、スイッチング電源の雑音を取り除きつつ、出力信号の余分な振動を抑えることができます。ただし、ダンピング抵抗を挿入することで消費電流が増えるというデメリットがあります。そこで、ダンピング抵抗と直列にC₂を挿入することで、直流電流がダンピング抵抗に流れるのを防ぎます。図2を見ると、共振による鋭い「ピーキング」が抑えられていることが一目りょう然です（赤線）。

　最後にカットオフ周波数とダンピング抵抗の計算式を紹介します。例えば、図1のR₁に抵抗素子、R₂にCを使った場合のカットオフ周波数は、R=1/ωCとなる周波数なので、f=1/（2πRC）となります。一方、ダンピング抵抗は共振周波数時のL（またはC）のインピーダンスと近い抵抗値に設定します。共振時のLとCのインピーダンスの大きさは等しく、Z=√（L/C）になります。ダンピング抵抗もこの値に設定します^＊2）。図3（c）では、L=159μH、C=15.9nFと設定したので、共振周波数は100kHzで、そのときのインピーダンスの大きさは100Ωになります。従って、ダンピング抵抗値も100Ωに設定します^＊3）。次回は、トランジスタや電界効果トランジスタ（FET）の活用方法を紹介します。

＊2） 不要な振動を完全に無くすには、もう少し複雑な計算が必要になります。

＊3） 図3（b）のようにスイッチング電源と組み合わせる場合は、負荷が接続されますので、その分を勘案してダンピング抵抗値を決めます。

→「Analog ABC（アナログ技術基礎講座）」連載一覧←

Profile

美齊津摂夫（みさいず せつお）

1986年に大手の通信系ハードウエア開発会社に入社し、光通信向けモジュールの開発に携わる。2004年に、ディー・クルー・テクノロジーズに入社。現在は、同社の常務取締役CTO（最高技術責任者）兼プラットフォーム開発統括部長を務めている。「大学では電気工学科に所属していたのですが、学生のときにはアナログ回路の勉強を避けていました。ですから、トランジスタや電界効果トランジスタ（FET）を使ったアナログ回路の世界には、社会人になってから出会ったといっていいと思います。なぜかアナログ回路の魅力に取りつかれ、23年目になりました」（同氏）。

関連キーワード

回路 | 電源 | Analog ABC（アナログ技術基礎講座）： | トランジスタ | コンデンサ