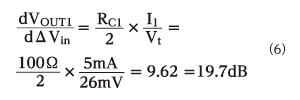第15回 差動対の利得を理解する:Analog ABC(アナログ技術基礎講座)(3/3 ページ)
今回は、差動対の利得に焦点を当てましょう。差動対は、例えばオペアンプなど、あらゆる増幅器の入力段に使われています。増幅器の重要な指標である利得について、理解を深めるのは大切なことです。
エミッタ接地の利得と同じ形
図1の差動対の利得を具体的に計算すると、以下のようになります。
図1のV2に信号を入力したときの周波数特性を図4(a)に示しました。エミッタ電圧Veの周波数特性は、−6dB(1/2倍)で一定となっています。
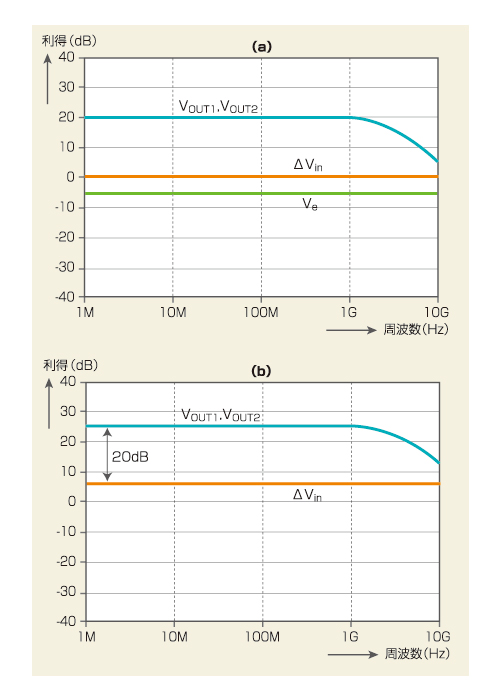
図4 差動対の周波数特性 (a)は、片方のトランジスタのみに信号を入力したときの周波数特性。(b)は、2つのトランジスタに、位相を反転させた信号を入力したときの周波数特性です。VOUT1とVOUT2は同じ周波数特性のため、曲線が重なって1本に見えています。
これは、トランジスタQ1のエミッタ側の等価抵抗Re1と、Q2のエミッタ側の等価抵抗Re2に入力信号が分圧されて、入力信号の振幅に対して、半分の振幅がエミッタVeに発生していることを示しています。
さらに、トランジスタQ1のベースだけではなく、Q2のベースにも信号を入力してみましょう。ただし、Q2の入力信号は、Q1の入力信号に対して位相を反転させます。この場合、トランジスタが左右対称に動作しているため、エミッタ電圧Veには、信号が表れません(図4(b))。図4(b)では、グラフの下にはみ出ているため、Veは表示されていません。実は、エミッタ電圧の振幅は、左側のトランジスタQ1と右側のトランジスタQ2で相殺されて、ゼロとなっているのです。
また、VOUT1とVOUT2の利得は、Q1とQ2の両方に信号が入力され、差動対の入力振幅ΔVinが6dBアップ(2 倍)するため、約26dBになります*1)。差動対では、入力信号の位相を反転させて対称に入力すると、(6)式に示した1/2がなくなり、エミッタVeを接地したエミッタ接地増幅回路と同じ特性になることが分かります。
次回は能動負荷を活用
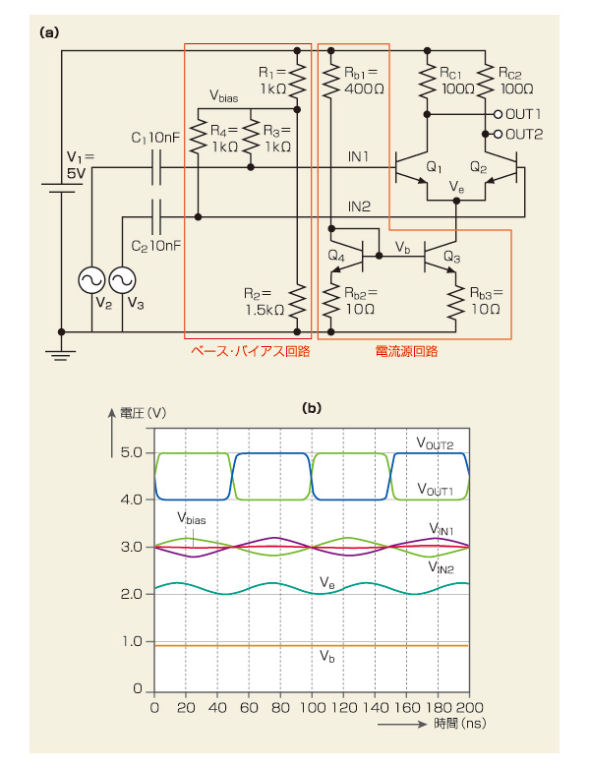
図1の差動対にベース・バイアス回路と電流源回路を入れて、実際の差動対に少し近づけてみました(図5(a))。別の機会に紹介したいと思いますが、電流源には「カレントミラー回路」を使いました。ベース・バイアス回路は、シンプルな抵抗分割回路です。
図5(b)に、図5(a)の各部の信号波形を示しました。入力信号の差(Vin1−Vin2)に対して信号が増幅されており、これまで説明してきた通りの動作をしています。ところが、図5(b)をじっくり見ると、おかしな点に気が付きます。トランジスタQ1とQ2に対称に信号を入力したのにもかかわらず、エミッタ電圧Veが表れています。図4(b)に示した周波数特性では、エミッタ電圧Veは表れていませんでした。
回路をどこか間違えたのでしょうか。これは、回路の間違いではなく、シミュレーションの種類が違うために発生したものです。周波数解析(AC解析)は、動作点の状態が無限に続いている理想的な線形回路と仮定して解析するので、図5(b)のような非線形に変化する信号は計算できないのです(本連載の第11回を参考にして下さい)。
過渡解析はシミュレーション時間が長いので、シミュレーション時間が短い周波数解析で済ませてしまいたいのですが、実際に回路で起きている現象は過渡的な波形です。過渡解析に表れている波形が真の姿ですので、面倒でも過渡解析をしないと思わぬ落とし穴にはまることがあります。
次回は、「能動負荷」を使って、利得をさらに高め、実際のオペアンプに近づけましょう。利得を高めるには、コレクタ電流を増やす、増幅回路を多段接続する、コレクタ抵抗を大きくするという方法があります。能動負荷は、消費電力やトランジスタの寸法などを考慮すると最も効果的です。
Copyright © ITmedia, Inc. All Rights Reserved.