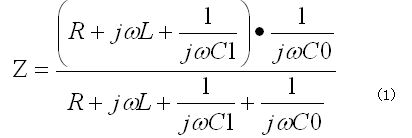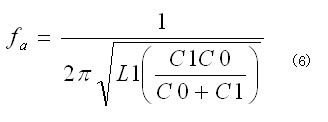第5回 水晶振動子の動きを等価回路で見る： 水晶デバイス基礎講座（1/2 ページ）

[宮澤輝久，セイコーエプソン]

　今回は、電気的な等価回路を使って、水晶振動子を考察しましょう。水晶振動子の機械的な振動は、電気的な等価回路でうまく表現でき、等価回路を使うことで挙動をより理解しやすくなります。また、水晶振動子を振動させる発振回路は、当然のことながら電気的な回路ですので、水晶も電気的な回路で表現すると都合がよいのです。

機械・音響の力学的な振動系と交流電気回路について、力学振動系と電気系を同様の等価回路で統一的に取り扱うことができます。これを、「電気機械音響類似」と呼びます。後ほど、詳しく説明します。

　水晶振動子が共振し、振動しているときの電気的な等価回路を、図1に示しました。図1（a）は、一般的な電気的な等価回路を表しています。高周波部品ですので水晶チップと保持器（パッケージ）の間に浮遊容量が発生します。しかし、図1（b）のように簡略化した等価回路を使用しても問題はありません。

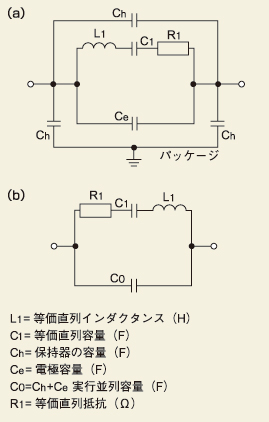
図1　 水晶振動子の等価回路　（a）は、一般的な電気的な等価回路を表しています。高周波部品ですので水晶チップと保持器（パッケージ）の間に浮遊容量が発生します。ただ、（b）のように簡略化した等価回路を使用しても問題はありません。

　図1（b）において、それぞれの記号の物理的な意味を説明しましょう。まず、等価直列静電容量（C1）は、機械的な運動に置き換えて考えるとバネやゴムの弾力に相当するもので、「水晶チップのコンプライアンス」と呼びます。

　物体の伸縮性や可塑性を定量化した物理量を、「機械コンプライアンス」、または「コンプライアンス」と呼びます。単位はメートル毎ニュートン （m/N）です。電気機械音響類似では、コンプライアンスは電気系の静電容量に相当します。水晶チップの等価直列容量（C1）を、水晶のコンプライアンス、または水晶の等価コンプライアンスとも呼びます

　次に、等価直列インダクタンス（L1）は、機械的な運動に置き換えると振動している部分の質量に相当します。等価並列容量（C0）は、浮遊容量も含めた電極間の静電容量です。

　等価直列抵抗（R1）は、振動時の内部摩擦や水晶チップの支持系の機械的な損失、音響損失といった振動エネルギーの損失成分を表しています。R1が、これまで何回か出てきたCI（クリスタルインピーダンス）値に相当します。

等価回路から発振周波数を計算

　次に、電気的な等価回路を使って、水晶振動子の発振周波数について考察してみましょう。図1（b）に示した水晶振動子の電気的な等価回路には、位相がゼロになる2つの周波数が存在します。直列共振周波数（fr）と、並列共振周波数（fa）です。

　早速、直列共振周波数（fr）と、並列共振周波数（fa）を求めてみましょう。まず、図1（b）に示したR1とC1、L1の直列とC0で構成した直並列回路のインピーダンスを求めます。

位相がゼロになる2つの周波数を見つけ出すために、（1）式を実部と虚部に分け、虚部＝0とします。虚部＝0を変形してまとめると、（2）式になります。

ここで、R²＜＜ωC0なので、

虚部＝0となる周波数は、以下の2つの式で計算できます。

従って、2つの共振周波数frとfaは、以下の式となります。

　一般的な水晶振動子では、等価直列容量（C1）≪　等価並列容量（C0）となり、faは結果として（8）式のように表現できます。C0とC1の比は200〜400程度ですので、faはfrよりもわずかに高い周波数になります。

平方根の部分を級数展開して、1次の項までを考慮すると、