グラフェンでツルツルに、水が素早く通過する：第3の微細加工技術（1/4 ページ）

グラフェンを利用した微細デバイスに不思議な性質が見つかった。パイプの直径が狭くなると、一般に水が内部を流れにくくなる――このような常識を覆す結果だ。グラフェンの世界的権威である英マンチェスター大学のAndre Geim氏が率いる研究チームが実証した。「ファデルワールスアセンブリー技術」を適用、製造したデバイスを用いた。分子ふるいとして応用でき、海水の脱塩処理や半導体製造にも役立ちそうだ。

[畑陽一郎，EE Times Japan]

ノーベル賞とイグノーベル賞を双方受賞

　ノーベル賞とイグノーベル賞^＊1）の両方を受賞した研究者が1人だけいる。ロシア出身のドイツ系物理学者Andre Geim氏だ。同氏は2001年から英マンチェスター大学で物理学の教授としてグラフェンの研究を率いている。

　Geim氏と同大学のポストドクトリアル研究者であるRadha Boya氏が率いる研究チームが2016年9月7日に発表した研究成果は、2つある。1つは微細な構造物である分子サイズのトンネルを計算通り正確に作り上げたこと（図1）。目に見えるサイズのグラファイトと数層のグラフェンを「貼り合わせ」ることで実現した。

　もう1つはこのトンネルが持つ奇妙な性質を発見したこと。予想に反して、物質が内部を高速に流れる。重力で水が滴下するような条件では、流速は秒速0.1m程度と速いことが分かった^＊2）。

＊1） 水のもつ反磁性を示すために16T（テスラ）の磁力を与えて小さなカエルを空中浮遊させた実験により、2000年、Michael Berry氏とともにイグノーベル賞を受賞（カエル体内の水の反磁性を利用）。Konstantin Novoselov氏とともにグラフェンに関する革新的な実験により、2010年にノーベル物理学賞を受賞。Geim氏は研究の幅が広いことでも知られている。例えば、「Gecko tape（ヤモリテープ）」の試作だ。ヤモリは、後述するファンデルワールス力を利用した「毛」を使って垂直なガラスの表面を歩く。この原理を用いた。
＊2） 水に1000気圧まで圧力を加えた場合、細管の中を水が秒速1mで流れる。

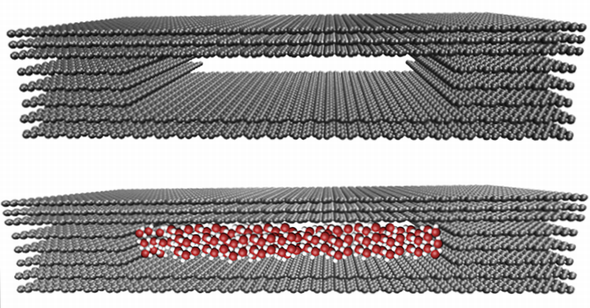
図1　試作したグラフェントンネルの構造と流体の関係　グラフェン3層分、およそ1.36nmの高さのパイプのモデル断面図（上）。このパイプに水（赤い酸素原子と白い水素原子からなる）を通すと、壁に接している水分子の比率が高いにもかかわらず、非常に速く流れる　出典：英University of Manchester

　今回の研究が生み出す果実も2つある。1つは実際的なものだ。細管を高速に水が流れるなら、「分子ふるい」として役立つ。海水から真水を得る脱塩処理の効率が高くなりそうだ^＊3）。水以外の液体やガスの分離にも役立つだろう。半導体製造や分子機械にも応用できそうだ。

　もう1つは理論的なもの。これまでにもグラフェンを含む分子レベルで微細な管の試作例があったものの、表面が原子レベルではデコボコだったり、測定器具との接続に問題があったりしたため、理論と実験の食い違いがはっきりしなかった。

　今回の実験では原子レベルで平滑な管を使っており、理論と実験がよく合致し、今後の研究ポイントを絞ることができた。「nanofluidics（ナノ流体力学）」が発展していく助けになるだろうとGeim氏は考えている。

＊3） 直径1nm未満の微細な穴が空いた逆浸透膜を用い、海水側に圧力をかけると海水の塩分を除去できる。樹脂膜を用いた実用装置では、海水に50気圧以上の圧力をかけており、圧力が高いほど、処理が早く進む。

カーボンナノチューブで異常が起きる

　Geim氏が微細な管に興味を持った理由の1つは、カーボンナノチューブ（CNT）研究で続く論争だ。CNTは炭素原子だけからなる直径0.4nm以上の細い管状分子。炭素原子が6角形状に結び付いた網からなる分子パイプと表現できる。

　論争の内容はこうだ。CNTに水を通した少数の実験結果によれば、通過速度が異常に高い。一般に管を通過する流体は、管の径が細くなればなるほど粘性の影響が高くなり、毛細管ではほとんど流れない。理論的な分析や分子動力学（MD）^＊4）に基づいたシミュレーションでは、速く流れるという予測があったものの、微細な管を使った実験装置が正しく動いているかどうかに疑問があり、実験結果がおかしいのではないかという声が出ていた。

　Geim氏はCNT同様、6角形状に炭素原子が結び付いたグラフェンを使って微細な管を作り上げ、この現象を調べた。

＊4） 分子動力学の手法は以下の通り。多数の分子（原子）を要素として、初期配置を決める。その状態である分子が他の全ての分子から受ける引力と斥力を計算し、全分子の次の配置を決定する。ごく短い時間間隔でこのような計算を繰り返し実行し、集団としての運動を予測する。