困惑する人工知能 〜1秒間の演算の説明に100年かかる!?：Over the AI ――AIの向こう側に（7/8 ページ）

コンピュータは、入力値から出力値に至る演算のプロセスを、順番通りに説明できます。ところが、「なぜ、その結果になったのか」と尋ねると、途端に説明できなくなってしまいます。困惑し、黙りこくったり、自分が行った演算を“言い訳”のごとく延々と説明したりと、迷走を始めるのです。

[江端智一，EE Times Japan]

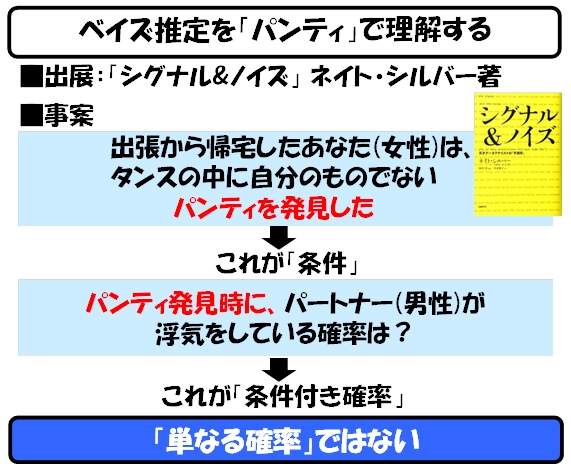
「パンティ問題」で定理を導く

　では、今回もネイト・シルバーさんの「シグナル＆ノイズ」のネタを使わせていただいて、ベイズ推定の話をしたいと思います。

　ここからの説明の目的は、パートナー（男性）の浮気の確率が、他の条件によって（タンスの中からパンティが発見されたという事実で）変化することを理解していただくことです。

　まず、この問題を検討するに際して、以下の確率情報が与えられているもの（Given）とします。

　上記のケースでは、（1）は統計的かつ客観的なデータから導かれた確率ですが、（2）（3）はエイヤ！　で、値を決めています。本来は、データから導かれていることが望ましいので、一応、「パンティを発見した時の浮気の数値データ」をネットで探しましたが、見つけられませんでした（もっとも、その手の記事は山ほど見つかりましたが）。

　さて、「シグナル＆ノイズ」では、ここからいきなりベイズ推定の話になっているのですが、私はここで、具体的な数値に落して説明してみたいと思います。

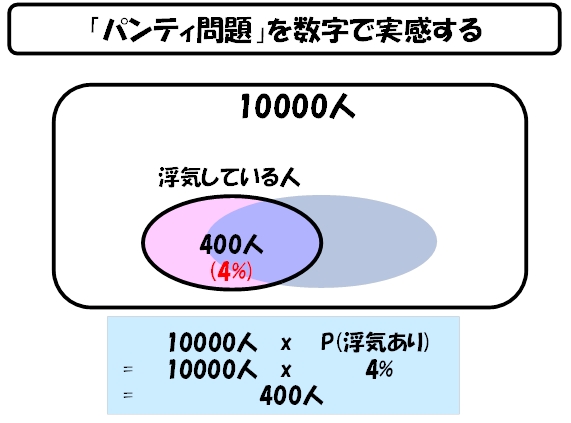
　確率で語ると分からなくなるので、「横浜スタジアムに集まった1万人の既婚男性が、『アメリカ横断ウルトラクイズ』形式で質疑応答をする」というイメージで、考えてみましょう。

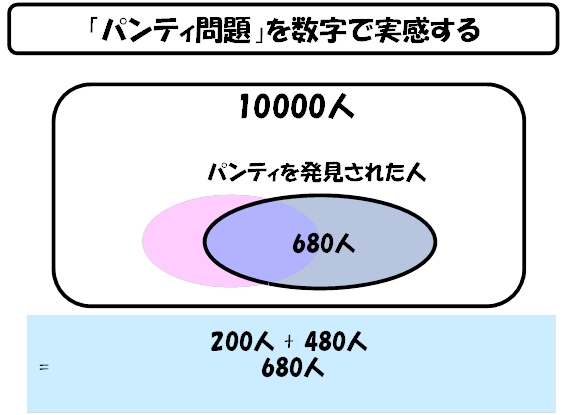
　まず、1万人の既婚男性のうち、デフォルトで4％が浮気をしているので、400人が浮気をしていることになります（下図）。

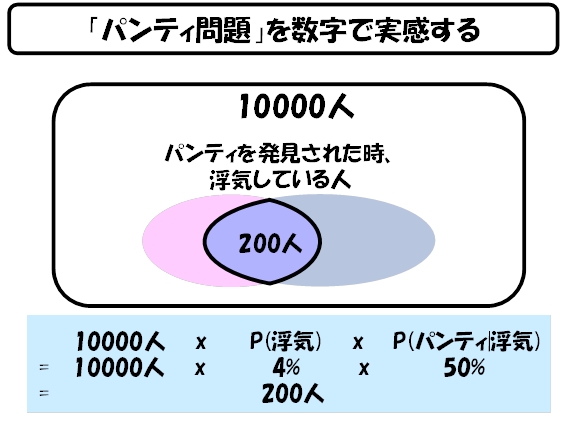
　次に、奥さんにパンティを発見された時に、浮気をしている人は200人になります。これは、前述の浮気をしている人が、パンティを残しているという（仮想の）確率50％から導きます（下図）。

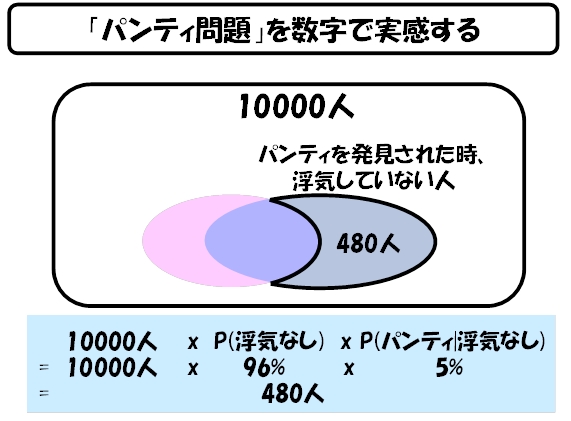
　さらに、パンティを発見された時に、浮気をしていない既婚男性は、480人になります。これも前述の、浮気をしていなくても、女性のパンティを残しているという ―― いわゆる女装癖か、あるいは、奥さんへのサプライズギフトを考慮した（仮想の）確率5％から導きます（下図）。

　さて、ここで、浮気をしていようが、浮気をしていまいが、とにかく、奥さんにパンティを発見されてしまった人は、680人（=200人+480人）となります（下図）。

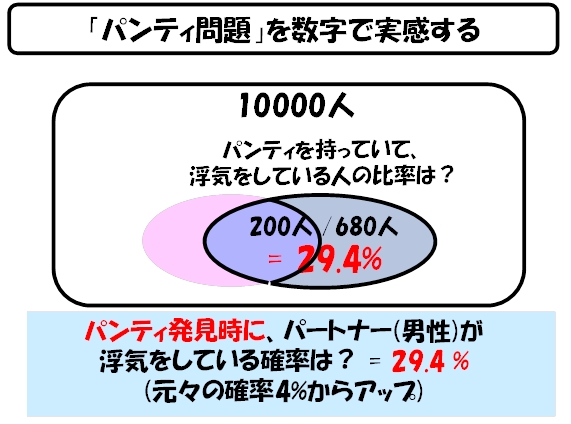
　ここから、パンティを奥さんに見つけられた（680人）という条件下において、本当に浮気をしていた人（200人）の確率として、200÷680である、29.4％が導かれることになります。

　つまり、妻は、「夫は4％くらいの確率で浮気するもの」、と常に心に留めておかなければなりませんが、ここに「パンティ発見」という事実が発生した瞬間、この浮気の確率が29.4％に跳ね上がる ―― 事後的に確率が変動する ―― という事実が、数学的に確認されたことになるわけです。

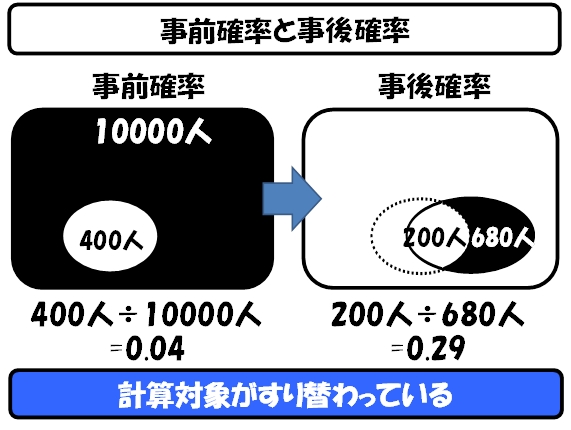
　この事前確率と事後確率の関係を比較したものが下図です。このように母集団の数が変っているのではなく、確率に条件が付いたことで、確率計算の対象が、すり替わっていることが分かります。

　さて、「数式ゼロ」のAI解説としてはふさわしくありませんが、この「パンティ問題」から、「ベイズの定理」を導き出せることを示します。

　「ベイジアンネットワーク」の解説の前半は、この「ベイズの定理」の考え方までとします。

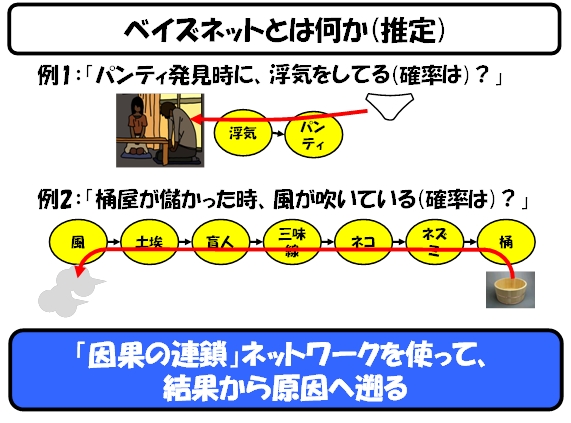
　次回、後半では、ベイジアンネットワーク（別称、ベイズネット）の考え方を、私がこれまで使ってきた具体的な事例を含めて、お話したいと思います（下図は次回掲載予定の図です）。