至宝の人工知能 〜問題に寄り添い、最適解をそっと教えてくれる：Over the AI ―― AIの向こう側に（17）（6/8 ページ）

先人たちにより開発され、磨かれてきた「至宝の最適化アルゴリズム」。本当はこれを軽々しく「AI」とは呼びたくな……い……という気持ちをぐっとこらえ、AI技術として解説します。「試験前の一夜漬け」「雪山遭難」「井戸堀り」の例を使って、説明していきます。繰り返しますが、最適化アルゴリズムを軽々しく「AI」という言葉で片付けたくはないんですよ、本当は。

[江端智一，EE Times Japan]

最適化アルゴリズムの非線形計画法を“雪山の遭難”で考えてみる

　では、次に、非線形計画法の考え方の一例をご紹介します。

　これは、雪山で遭難し、夜間の急激な温度低下で、翌朝までの生存の確率が絶無に近いと判断した時のパラダイムで説明することができます。

　ブリザードを避けるような場所もない登山者は、危険を承知で下山を決意します。

　ただし、暗闇と吹雪で視界ゼロ。地図もなく自分の位置も不明。登山者が知り得る情報は、その方向が「上り」か「下り」か、そして、その角度（斜度）だけです。

　この時に、登山者のとり得る戦略は1つしかありません。その場、その時における、下り傾斜が最大の方向に降りていくことだけです。これを、「最急降下法」といいます。

　このシンプルな方法では、最短時間で下山に成功する確率が最も高くなりますが、しかし、最も急な斜面を下ったところで、そこが単なる谷底だったという場合もあります。こうなると、どの方向に向いても、下ることができなくなり、私の死亡は確定的です。

　この状態を、局所的最適解（ローカルミニマム）に陥ったといいます。

　このように、最急降下法は、初期値（遭難した場所）によって、大域的最適解（山小屋）に到達できるかどうかが、確定的に決まってしまうのです。

　最適化アルゴリズムの研究の歴史とは、乱暴にまとめれば、この「ローカルミニマム」との闘いであった、とも言えます。

　そこで、いろいろな方法が考案されてきました。

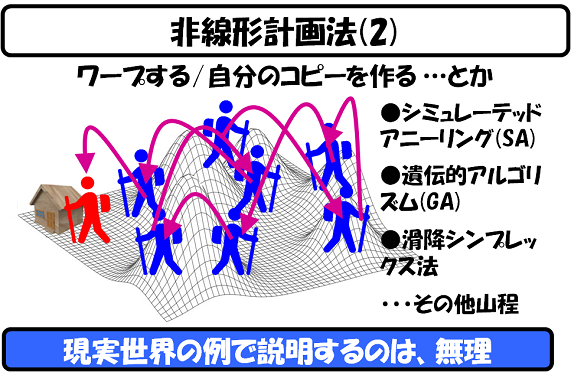
　例えばシミュレーテッドアニーリングという方法は、下山時開始時にはポンポンと空を飛ばせて、遠くの下山場所に変化させ、凍死直前には、飛ばないようにすることで、山小屋への到着率を高める、というものです（『空を飛ぶ体力があるなら、下山は簡単だろう』というツッコミは無しの方向で。これは、最適化アルゴリズムの話です）。

　また遺伝的アルゴリズム（GA）^＊）は、自分のクローンを大量生産して、全員で下山情報を共有するというものです（『そんな魔法が使えるなら、下山は簡単……』（以下省略））。

＊）関連記事：「抹殺する人工知能 〜 生存競争と自然淘汰で、最適解にたどりつく」

　「最適化アルゴリズム」は、解決する問題にベッタリと寄り沿って、その問題を解くための「最適化」を極めるアルゴリズムですが、いくつかの問題点があります。

　第1の問題点は、前述した通り、問題に応じた適当なアルゴリズムを選ばなければならないことが挙げられますが、これは、踏んできた場数（試してみたアルゴリズムの数）に影響を受けます。

　第2の問題点は、強化学習とは真逆の発想で「課題や解法を完璧に理解しないと使えない」点も挙げられます（当然ですが）。

　さらに、第3の問題点は、計算終了時間が、事前に読み切れないということです。「これまで、1分間で解けていた問題に、未知数をたった1個追加しただけで、計算時間が100年を超えることになってしまった」、なんてケースは、ざらにあります（あまり驚くことではありません）。