不幸な人工知能 〜尊敬と軽蔑の狭間で揺れるニューラルネットワーク：Over the AI ―― AIの向こう側に（21）（6/9 ページ）

今回のテーマは、第3次AI（人工知能）ブームを支えているといっても過言ではない花形選手、ニューラルネットワークです。ただしこのニューラルネットワーク、幾度もダイナミックな“手のひら返し”をされてきた、かわいそうなAI技術でもあるのです。

[江端智一，EE Times Japan]

ニューラルネットワークは何がすごいのか

　ニューラルネットワークの凄さは、その非線形分離の能力にある、ということを説明しましたが、もう少しだけ突っ込んだお話をします。

　私が、ニューラルネットワークを知ったときに驚いたのは、XORの入出力を分離できる、ということでした。XORとは、論理回路の一種で、z = f（x,y）の問題において、（x,y,z）が、（0,0,1）, （1,0,1）, （0,1,1）, （1,1,0）となる論理回路のことです。

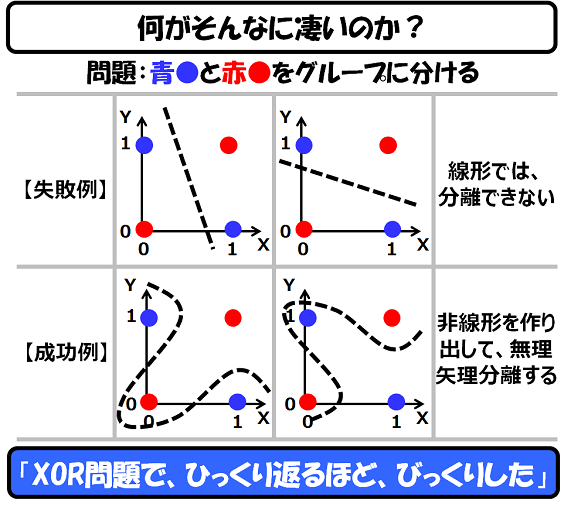
　まあ、簡単に言うと以下の図において、以下の4点を2つのグループに分ける問題です。

　この図を見ていただければ明らかですが、この青と赤の点は、直線では分離できません。曲線なら可能ですが、このような曲線を作る関数を作るのは面倒です。もっともXOR程度であれば、頭の中で非線形関数を作ることは簡単ですが、これが、もっと複雑なデータ（例えば、次元数の大きいデータ）となると、人間の頭では理解できなくなります。

　ニューラルネットワークの価値は、「直感的にイメージできない、高次元の空間を使って分離ができるように矯正できる」という点にあります。この「矯正」が「学習」と呼ばれているものです。

学習が“運頼み”!?

　このような高次元の空間の分離を可能とする多層ニューラルネットワークは、学習によって作られますが、いつでも必ず学習に成功するというわけではありません。例えば、たかだか4点しかないXORですら分離できない ―― つまり、学習できないことがあるのです。

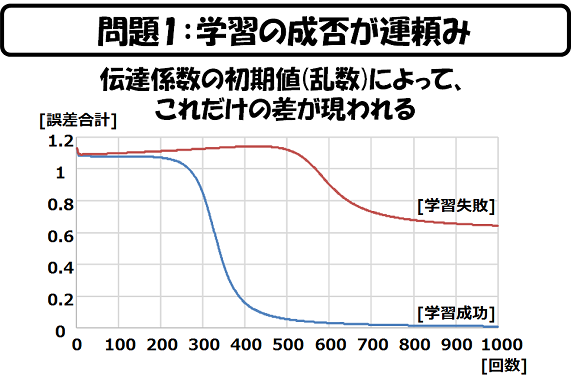
　下図は、私が作った入力層2ノード、中間層2ノード、出力層1ノードのニューラルネットワークのプログラムで、実際にXORの学習データを学習させて、その収束状況（誤算の変化）を示したものです。

　シナプス値の初期値は乱数によって決めることが多いのですが、ある乱数では、あっというまに学習が完了（誤差がなくなる）し、別の乱数では、全く学習が完了しないことあるのです（私の経験では、学習が完了しないケースの方が圧倒的に多いです）。

　つまり、学習の成否が「運頼み」ということです。

　私は、大学の修士論文のテーマを、「ニューラルネットワークの活用手法」としていたのですが、ニューラルネットワークがうまく学習してくれなくて（誤差が収束しなくて）、胃の痛む毎日を送っていました。

　最終的には、大学の計算機センタのコンピュータを使って、学習に成功する初期値を探す、という、誠にもって本末転倒なことを続けていました ―― この頃に、私のニューラルネットワークに対する不信感が芽生えはじめます。

　本当にたまたま学習に成功した場合であっても、ニューラルネットワークの出力結果を調べてみたら、これがもう、お話にならないくらいひどいものでした。