投資初心者が見つけた“黄金の組み合わせ”：「お金に愛されないエンジニア」のための新行動論（5）（3/7 ページ）

2022年初頭から、“投資初心者”として、投資の勉強をひたすら続けてきました。その初心者の私に最も適した投資の方法としてたどり着いたのが、インデックス投資です。ランダムウォーク分析×現代ポートフォリオ理論という“黄金の組み合わせ”から成るものです。

[江端智一，EE Times Japan]

株価は予想できない、という潔い諦めが出発点

　さて、ここから、今回のコラムの本命、（D）ランダムウォーク分析の話に入ります。

　前回のコラムの復習ですが「ランダムウォーク」とは、要するに、泥酔して意識のない酔っ払いの、規則性のない歩き方のことです。

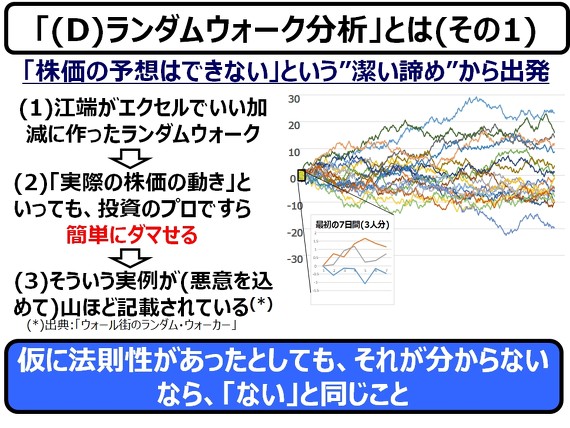
　ここから「株価の変動に、法則性を期待してもムダ」という割り切りが、ランダムウォーク分析の根底にあります。

　『ウォール街のランダム・ウォーカー』には、コインの裏と表をグラフにしただけのものを見て、『これは、○○のパターンにマッチしているね！（テクニカル分析による）』てなことを熱く語った人に、その後、その真相（単なるコイントスの結果）を語って気まずくなったという話が記載されています。

　ちなみに、上記のグラフの一つに某総合電機メーカーの株価を紛れこませています。それを発見できた人は、江端にご連絡ください。

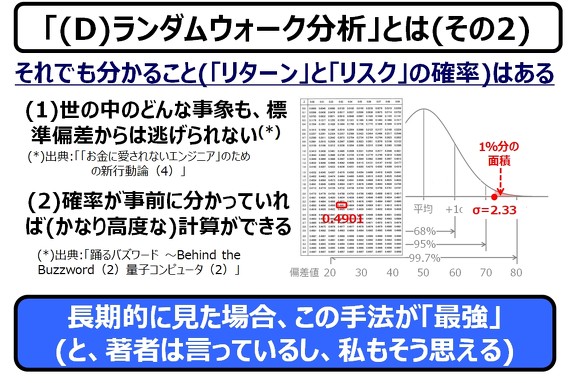
　「株価の変動に、法則性を期待してもムダ」といいつつ、ランダムウォークであっても、分かることはあるのです。

　つまり、酔っ払いのランダムウォークであっても、今から、1分後に、現在地から200メートル先に移動していることは『絶対にない』と言えます（秒速3.3メートル、時速12kmの歩行）。しかし、60メートル先なら、相当に低い可能性ですが、『ない』とは言えません（時速3.6kmのしらふの歩行になりますが）。

　要するに、これが、標準偏差の考え方です。標準偏差と平均値を使えば、リスクとリターンが、算出できます。『ウォール街のランダム・ウォーカー』の著者は、それらをうまく使って運用している「インデックス投資が、最強である」と断言しています（この話は、後半に続きます）。

投資心理と金融工学

　さて、ここまでは、4つの投資分析の手法についてお話しましたが、ここからは、私が、つまみ食い的に（×体系的に）調べてみた2つの投資理論、行動ファイナンス理論と、現代ポートフォリオ理論について説明してみたいと思います。

　先程の4つの分析と、この2つの理論の何が違うかというと、分析は「やり方（メソッド）」、理論は「考え方（セオリー）」くらいだと思ってください。

　「行動ファイナンス」の考え方を使って「テクニカル分析」をしてもいいし、「現代ポートフォリオ理論」を使って、「ファンダメンタルズ分析」をしてもいい、という感じで把握しておいていただければ十分です ―― と言うか、私もキレイには分けて考えることはできていません。

　さて、行動ファイナンス理論と現代ポートフォリオ理論の違いは、それぞれ、投資心理（心理学）と金融工学（数学）の違い、と説明できます。

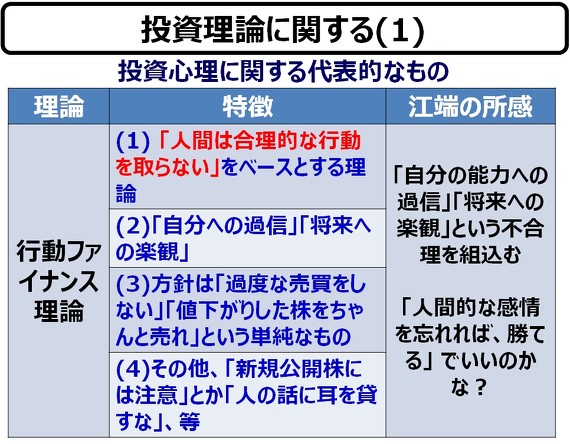
　まずは「行動ファイナンス理論」について、ざっくりと説明します ―― なぜ「ざっくり」なのかというと、「行動ファイナンス理論」を定式化した文献を、（私は）見つけられなかったからです。

　人間は合理的な行動を取らない ―― 行動ファイナンス理論は、この一言に尽きます。これは前述の「アノマリー分析」とも関係があります。

　なにしろ、投資家という人間は、

• 値下がりしている株を買おうとはしないし、それどころか、逆に売ろうとするし、
• 逆に、値上がりしている株に殺到するし、

など、古典経済学から言えば、人間は非合理で愚か者の役割を演じているだけです。その癖、『自分だけは、市場を出し抜いてやる』と真面目に信じているのですから、投資家というのは、本当に救いがたい人間です。

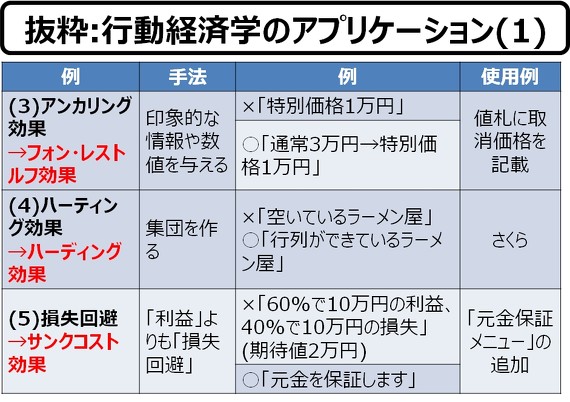
　この投資心理を調べているうちに、以前調べた「行動経済学」と似通っていることに気が付きました。案外、「行動経済学」というのは、市場の金融商品に対する、投資家の非合理なアクション（わけの分からん投資モチベーション）を理解するために、生まれてきたのかもしれません（裏は取っていません）。

　行動経済学のアプリケーションについては、「未来を占う人工知能 〜人類が生み出した至宝の測定ツール」に記載していますので、ここでは、一部のみを抜粋・紹介します。

　プロの投資家の投資行動が、行動経済学のアプリケーションに含まれるのであれば、プロの投資家も私たち素人も、その知性や判断力においては大して変わりはない、と言えるかもしれません。