第3回 回路はすべてオームの法則から（後編）：Analog ABC（アナログ技術基礎講座）（1/2 ページ）

[美齊津摂夫，ディー・クルー・テクノロジーズ]

→「Analog ABC（アナログ技術基礎講座）」連載一覧

　前回は、アナログ回路を理解する上で、最も重要で、基本的な法則であるオームの法則と、オームの法則に現われるインピーダンスについて説明しました。今回は実際に、抵抗（R）やインダクタ（L）、コンデンサ（C）の直列回路や、並列回路のインピーダンスを考察し、そこに現われる現象を調べてみます。

　これらの回路では、インピーダンスが極端に大きくなったり、小さくなったりする「共振」と呼ぶ興味深い現象が、ある決まった周波数で発生します。抵抗とインダクタだけ、あるいは抵抗とコンデンサだけでは作り出せない、無限大やゼロに近い大きさのインピーダンスを生み出すことができるのです。共振現象をうまく利用すれば、特定の周波数の信号だけを抽出するフィルタ回路や、周波数精度が高い発振回路などに応用できます。そこで今回は共振現象について解説しましょう。

LとCの勝負

　図1（a）に抵抗とインダクタ、コンデンサの直列回路、図1（b）に並列回路を示しました。これらの回路のインピーダンスは周波数に対してどのように変化するでしょうか（図1（c））。図1（a）は直列回路なので、全体のインピーダンスの大きさは、抵抗とインダクタ、コンデンサそれぞれのインピーダンスの和になります。従って、インピーダンスが大きい素子の影響が強くなります。

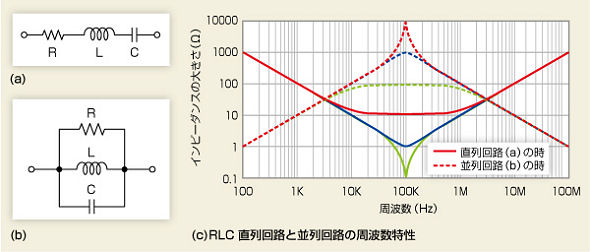
図1　RLC直列/並列回路の周波数特性　RLC直列回路（a）と、RCL並列回路（b）のインピーダンスの周波数特性を（c）に示しました。グラフの色の違いは純抵抗成分の値の違いを意味します。共振周波数は100kHzで、このとき直列回路ではインピーダンスが最も小さくなることが分かります。純抵抗成分が無い場合にはゼロに近づきます。一方、並列回路ではインピーダンスは最も大きくなります。抵抗成分が無い場合には、無限大に近づきます。

　そうなると、前回説明したように、周波数が低い場合ではコンデンサのインピーダンスが大きくなり、コンデンサが「勝ち」ます。反対に高周波数側では、周波数が高くなるにつれてインピーダンスが大きくなるというインダクタの特徴が回路全体に現われます。インダクタが勝っているのです。

　それでは、低周波数側と高周波数側の中間部分では、どちらが勝つのでしょうか。中間部分のある特定の周波数では、コンデンサとインダクタのインピーダンスの大きさが近づき、お互いに譲らずに主張し合うことになります。まさにこのとき、コンデンサ単体のインピーダンスやインダクタ単体のインピーダンスよりも、回路全体のインピーダンスははるかに小さくなるのです。これが「共振現象」で、この現象が発生する周波数が共振周波数です。

　図1（c）を再び見てみましょう。横軸は周波数で、縦軸はインピーダンスの大きさです。100kHzより低い周波数では、コンデンサが勝っているので右下がりの傾斜に、100kHzより高い周波数ではインダクタが勝っているので右上がりの傾斜になっていす。ところが、ちょうど100kHz付近になると、互いがほぼ同じインピーダンスになって主張し合っています。この回路の共振周波数は100kHzであることが分かります。純抵抗成分Rが無いと、直列回路全体の共振時のインピーダンスは0に近づきます。

　一方、抵抗とインダクタ、コンデンサを並列につなぐと、共振周波数では、回路全体のインピーダンスが非常に大きくなります。並列回路の場合はインピーダンスの小さい素子が勝ち、回路全体にその影響が現れることになります。すなわち、低周波数側ではインダクタが、高周波数側ではコンデンサが勝ちます。その中間部分の共振周波数では、純抵抗成分Rが無い場合、インピーダンスは無限大に近づきます。