もはや怪談、「量子コンピュータ」は分からなくて構わない:踊るバズワード 〜Behind the Buzzword(1)量子コンピュータ(1)(7/9 ページ)
「業界のトレンド」といわれる技術の名称は、“バズワード”になることが少なくありません。世間はそうしたバズワードに踊らされ、予算がバラまかれ、私たちエンジニアを翻弄し続けています。今回から始まる新連載では、こうしたバズワードに踊らされる世間を一刀両断し、“分かったフリ”を冷酷に問い詰めます。最初のテーマは、そう、今をときめく「量子コンピュータ」です。
「量子ビット」を知ろう
では、量子論のことはスッパリ忘れて、量子コンピュータの話を始めたいと思います。
量子コンピュータも、今使っているパソコンなどのコンピュータと基本的には同じ仕組みで動きます。ちなみに、量子コンピュータに対して、現在のコンピュータを「古典コンピュータ」と言います ―― 現在世界中で活躍中のコンピュータを「古典」と言い切るあたり、ものすごいと思います。
コンピュータが"1"と"0"だけで動いていることは有名ですが、これは、実は0Vと5V(または3.3V)の電気の電圧を切り変えて実現しています。基本的には、トイレの電気をON/OFFすることと同じです。このON/OFFを行うスイッチのことを"ビット"、または"古典ビット"と言います。
このスイッチは半導体素子で実現されていて、そのスイッチを気が遠くなるくらい大量に搭載しているものが、大規模集積回路です。
一方、量子コンピュータも基本は同じです。前述の「気持ち悪い振る舞いをする量子(あるいは、量子のマネをするもの)」を具体化することで、量子コンピュータを実現します。
重要なことは、複数の状態を同時に所有することができるビットを作ることです。これが「量子ビット」です。
「古典ビット」は"0"と"1"の状態を維持するだけですが、量子ビットは、2つの状態をドタバタと(しかし、デタラメではなく正確無比に)変化させつつ、観測することによって状態をピタッと固定させることが必要となる、とんでもなく難しいビットです。
ここで量子ビットの状態を、シュレーディンガーの猫を使って表現してみます。
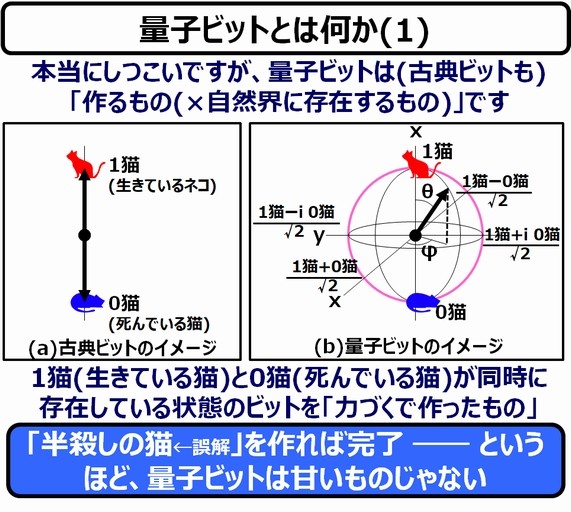
ここでは、古典ビットの"0"を死んでいる猫(0猫)、"1"を生きている猫(1猫)と表現することにします。この猫を使った場合、量子ビットでは、猫は下記(b)の球面上のどこかの一点に配置されます。これを、ブロッホ球といいます。
通常は"0猫"とか"1猫"などとは記載せず、ブラケット表記"|0>"、"|1>"を使います。これは、古典ビットの"0"と"1"と同じものと考えて、0猫" = "|0>" = "0"、"1猫" = "|1>" = "1"、と読み換えて頂いて結構です(多分)。今回は、"0猫"と"1猫"の表記で押し通します。
この球面のことは、後程説明するので、ここでは、「"0猫"と"1猫"が併存して存在する」状態ということだけ覚えておいてください。
ただ、このブロッホ球が、結構な誤解を生む原因となっています(少なくとも私は混乱しました)。
球面上の1点にある状態とは、量子ビットのように「停止している状態」ではなく、ドタバタと動いている状態を、振幅や位相差を使って見やすく表現したものなのです ―― うん、分からないですよね。そんなに簡単に分かってたまるものか(後程、もう一度説明します)。
では、いったんここでまとめてみたいと思います。
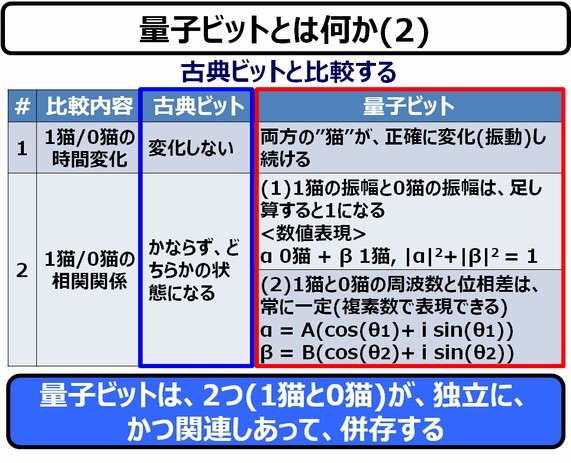
古典ビットは、"1"の状態(1猫)に対して何もしない限り、ずっと"1"のままです。"0"の状態(0猫)についても同じです。このビットを作るのは簡単です。真空管やトランジスタはもちろんですが、トイレのスイッチでもできます。2つの状態を作ればいいだけですから。
ところが、量子ビットは、こんな簡単ではありません。量子は放っておいても量子の振る舞いをしますが、それを量子コンピュータの量子ビットとして使うのであれば、上記の表の赤線で囲んだ部分の条件で動くようにしなければなりません。自然状態では、こんな都合よく動く量子はありませんので、このように動く量子ビットのデバイスを作らなければならないのです。
さてここで、量子ビットの説明に入る前に、波動の複素数表示について説明します。
前述した通り、量子ビットの状態はブロッホ球上の球面へのベクトル(矢印)で表現されますが、量子ビットは、つねに"0猫"と"1猫"がドタバタと動き回っている状態です ―― うん、私には、読者の皆さんが「江端が何言っているか分からない」が、手に取るように分かります。
では、以下の図で説明してみます。
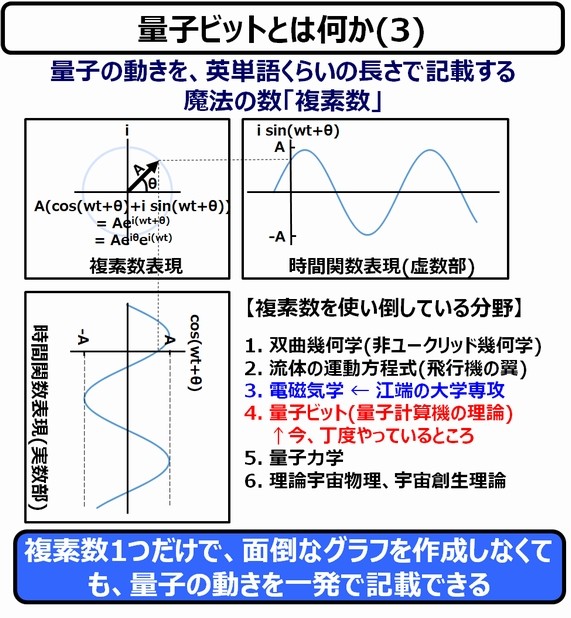
図の左上のベクトルが、いわゆる波動の状態(正確には波形の振幅)を示すのですが、実際の波は、このベクトルが、ものすごい速さでグルグル回っているのです(量子ビットの表現では、この速さを示す角速度wが登場していません。ここ注意しておいてください)。
さて、上図では、1つの波なのに、2つの波(cosの波とsinの波)が登場しており、実際に目で観測される波は実数の波(cosの波)だけです。では、何のために虚数の波(sinの波)もまとめて表現しているか ――については、私が調べている限り「これだ!」と説明できているものはありませんでした。
ネットで調べた範囲では、圧倒的多数で「オイラーの公式(後述)に放り込むだけで、計算がラクになるから」でした(面倒くさい波動計算が、魔法のようにラクになるのは確かです)。
しかし、これは虚数を説明するには直感的な回答にはなっていません。実は、虚数の扱いについては、次女(高校2年生)にも同じこと質問されたことがあり、私は答えに窮してしまいましたが、思い付きで次のようなことを言いました ――
江端:「錘(おもり)をつけたバネは、振動しつづけるよね」
次女:「うん」
江端:「でもって、伸び切った時のバネって、その瞬間、止まっているよね」
次女:「うん」
江端:「なんで止まったのに、また動き出そうとするんだろう。そこで止まり続けてもいいはずなのに」
次女:「それは、バネが伸び切って速度がゼロになった時に、弾性エネルギーが最大となっているからで……」
江端:「運動エネルギー保存法則的にはその通りだけど、エネルギー保存法則(の微分方程式)からは振動現象の一般解は、直接的には導き出せないんだよ」
次女:「……は?」
江端:「ところが、三角関数を当てあてはめるだけで、スルスルと一般解に展開できるてしまうんだ。ということは、バネは等速の回転運動をしていると考えることができる」
次女:「……回転運動? バネは直線運動でしょう」
江端:「回転運動を横から見れば、直線運動になる。つまり伸び切った時のバネは停止しておらず、虚数軸方向から見れば動いていると言うことができる」
と、説明しました。
実際に、津波や交流電流、そして波動方程式に至るまで、「波」に関わるものを、オイラーの公式eiθ = cos(θ) + i sin(θ)を使うと、四則演算はもちろん、微分、積分、全ての計算で、キレイに解が出てくることが分かっています。
取りあえず、量子状態を表現するために、複素数の中でも、特にオイラーの公式を使うということで、めちゃくちゃラクができる、ということだけ覚えておいてください ―― というか、量子の状態が回転運動をベースとしてドタバタ変わり続けている、ということだけご理解頂ければ十分です。
Copyright © ITmedia, Inc. All Rights Reserved.