第28回 カレントミラーで2つのMOSFETの歩調を合わせる：Analog ABC（アナログ技術基礎講座）（1/2 ページ）

前回紹介した増幅回路は、2つのMOSFETのしきい値（Vth）のわずかなずれが、利得や動作点に大きな影響を与えるという欠点がありました。今回は、欠点をどのように改善するかを紹介しましょう。

[美齊津摂夫，ディー・クルー・テクノロジーズ]

→「Analog ABC（アナログ技術基礎講座）」連載一覧

　本連載では、第25回以降、バイポーラトランジスタからMOSFETに話題を移し、MOSFETの基本動作や増幅回路を解説してきました。前回はMOSFETを使った増幅回路の負荷抵抗に能動素子を使うことで、利得を高められることを紹介しました。

　ただし、この手法には欠点もあります。それは、2つのMOSFETのしきい値（Vth）のわずかなずれが、利得や動作点に大きな影響を与えることや、応答速度が遅くなることです。今回は、この2つの課題をどのように改善するかを紹介しましょう。

しきい値のずれが悪影響を生む

　p型MOSFETとn型MOSFETのしきい値のわずかなずれが、利得や動作点に大きな影響を与える理由は、しきい値のずれがMOSFETに流れる電流の差になるからです。結果、出力電圧が電源Vddやグラウンド（GND）付近に張り付いてしまいます。これを解決するには、p型MOSFETとn型MOSFETのそれぞれに流れる電流を同じ値にする必要があります。

　前回紹介した増幅回路では、p型とn型MOSFETのそれぞれに流れる電流を、別々の受動部品で決めていました。具体的には、第27回の「n型MOSFETにp型追加して利得向上」の図2（a）に示した増幅回路のR1とR2、R3、R7です。そのため、しきい値のずれがそのまま、MOSFETに流れる電流の違いになって表れてしまっていました。そこで、今回はしきい値が変わってもMOSFETを流れる電流が変化しないように、カレントミラーを使います。

　カレントミラーについては、第15回の「差動対の利得を理解する」や、第16回の「差動対がオペアンプに変身（1）〜能動負荷で利得を高める〜」で紹介しました。カレントミラーを使えば、2つのMOSFETに同じ値の電流を流すことができます。

カレントミラーで電流値を合わせる

　図1に、カレントミラーを追加した増幅回路を示しました。図中の赤色の枠がカレントミラーです。MOSFETのM4とM6、そしてM3とM5がそれぞれカレントミラーになっています。M3とM5の間にR9がありますが、MOSFETのゲートには電流が流れませんので、2つのMOSFET（M3とM5）のゲート電圧は等しくなり、同じ値の電流が流れます。つまり、M4にはM6と同じ電流が、M3にはM5と同じ電流が流れます。

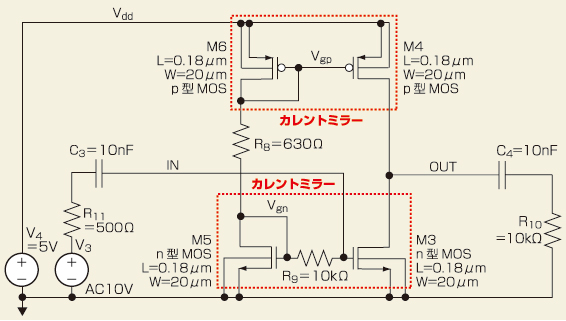
図1　カレントミラーを追加した増幅回路　前回紹介した増幅回路は、p型とn型MOSFETのそれぞれに流れる電流を、別々の受動部品で決めていました。そのため、しきい値のばらつきがそのまま、流れる電流の差になっていました。この現象をカレントミラーで防ぎます。

　それでは、M6とM5はどうかというと、これらのMOSFETにも同じ値の電流が流れます。ゲート電流が流れませんので、電源からM6に流れた電流はどこにも行けず、R8に流れるのです。R8に流れた電流も、他に流れ出す経路が無いので、M5に全て流れます。

　以上をまとめると、M3、M4、M5、M6の全てに同じ値の電流が流れていることになります。カレントミラーを使うことで、MOSFETのしきい値とは無関係に、2つのMOSFET（M4とM6）に同じ値の電流が流れるので、4つ全てのMOSFETに同じ値の電流が流れます。正確には、流れる電流の絶対値は、しきい値などで変化しますが、4つのMOSFETに同じ電流が流れることが重要な点です。

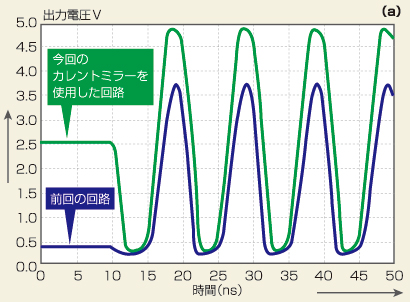
　図2（a）は、p型MOSFETのしきい値がn型に対して20mVずれた（−0.7Vが−0.72Vに変化）ときの出力波形です。カレントミラーを使わない前回の増幅回路では、出力電圧（図中の青の色のライン）はグラウンドに偏ってしまい、十分な振幅を得られていません。これに対して、カレントミラーを使った今回の増幅回路では、動作点が2つのMOSFETでずれず、十分な振幅を得られました（図中の緑の色のライン）。

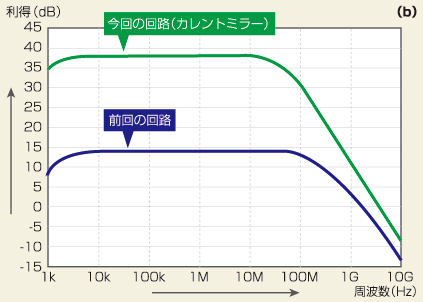
図2　カレントミラーを追加した増幅回路の効果　図上の（a）は過渡解析の結果です。前回は、出力電圧がグラウンド付近に張り付いていました。図下の（b）は、交流解析の結果で利得の周波数特性を示しています。カレントミラーを追加することで、しきい値がずれたときにも、利得を維持できます。

　図2（b）は、カレントミラーを使わない増幅回路と、カレントミラーを使った増幅回路の周波数特性です。カレントミラーを使わない増幅回路では動作点がずれていたため、十分な利得を得られませんでした。これに対して、カレントミラーを使うことで、しきい値がずれていないときと同じ利得を得られます。