Si基板を用いた窒化物超伝導量子ビットを開発:コヒーレンス時間を大幅に改善
情報通信研究機構(NICT)は、産業技術総合研究所(産総研)や名古屋大学と共同で、シリコン基板を用いた窒化物超伝導量子ビットを開発したと発表した。従来に比べコヒーレンス時間を大幅に改善した。
電極材料に超伝導転移温度が16Kの窒化ニオブを採用
情報通信研究機構(NICT)は2021年9月、産業技術総合研究所(産総研)や名古屋大学と共同で、シリコン(Si)基板を用いた窒化物超伝導量子ビットを開発したと発表した。従来に比べコヒーレンス時間を大幅に改善した。大規模量子コンピュータや量子ノードへの応用が期待される。
超伝導量子ビット材料としてこれまでは、アルミニウム(Al)とアルミニウム酸化膜(AlOx)を用いるのがほとんどであった。この場合、絶縁層として用いる非晶質酸化アルミニウムがノイズ源として課題になっていたという。
そこでNICTは、超伝導転移温度が16K(−257℃)の窒化ニオブ(NbN)と、エピタキシャル成長法で結晶化された窒化アルミニウム(AlN)絶縁膜に着目した。そして電極材料にNbNを、ジョセフソン接合の絶縁層にAlNをそれぞれ採用した、全窒化物のNbN/AlN/NbN接合を用いる超伝導量子ビットの開発に取り組んできた。また、窒化チタン(TiN)をバッファ層として用い、Si基板上にNbN/AlN/NbNエピタキシャル接合を行うことにも成功していた。
今回はこれらの技術を用いて量子ビット回路を設計、作製し評価を行った。実験に用いた基本回路は、量子ビットがマイクロ波共振器と結合した構造で、Si基板上にエピタキシャル成長させた窒化物超伝導体で作製した。
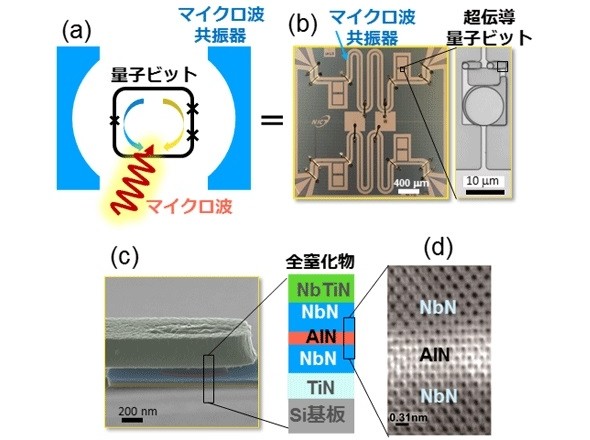
左上はマイクロ波共振器と量子ビットの概念図。右上は窒化物超伝導量子ビット回路の光学顕微鏡写真。左下は窒化物超伝導量子ビット(一部)の電子顕微鏡写真と素子の断面図。右下はエピタキシャル成長させた窒化物ジョセフソン接合の透過型電子顕微鏡写真 出所:NICT他
実験では、熱揺らぎが小さい10mKという極低温の環境で、量子ビットと弱く結合した共振器のマイクロ波伝送特性を測定した。この結果、コヒーレンス時間の指標となるエネルギー緩和時間(T1)は18マイクロ秒、位相緩和時間(T2)は23マイクロ秒であった。100回測定した平均値では、T1が16マイクロ秒、T2が22マイクロ秒となった。この値は酸化マグネシウム(MgO)基板上の窒化物超伝導量子ビットに比べ、T1が約32倍、T2が約44倍に相当するという。
NICTらは今後、「コヒーレンス時間のさらなる延伸」や「大規模集積化に向けた素子特性の均一性向上」を目指し、回路構造や作製プロセスの最適化に取り組む計画である。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 ゲノム解析データを安全に分散保管する実験に成功
ゲノム解析データを安全に分散保管する実験に成功
東芝と東北大学東北メディカル・メガバンク機構、東北大学病院および、情報通信研究機構は、量子暗号通信技術と秘密分散技術を組み合わせたデータ分散保管技術を開発、この技術を用いゲノム解析データを複数拠点に分散し安全に保管する実証実験に成功した。 テラヘルツ帯で動作する周波数カウンターを開発
テラヘルツ帯で動作する周波数カウンターを開発
情報通信研究機構(NICT)は、半導体超格子ハーモニックミキサーを用いたテラヘルツ周波数カウンターを開発し、0.1T〜2.8THzという4オクターブを超える帯域で精度16桁の計測を実現した。テラヘルツ帯の周波数領域は、「Beyond 5G/6G」での利活用が期待されている。 NICTら、ミリ波信号を光ファイバーに直接伝送
NICTら、ミリ波信号を光ファイバーに直接伝送
情報通信研究機構(NICT)は、住友大阪セメントや早稲田大学と共同で、ミリ波無線受信機を簡素化できる光・無線直接伝送技術を開発、受信した高速ミリ波無線信号を光ファイバーへ直接伝送することに成功した。 産総研ら、超伝導体でスピン配列の制御を実現
産総研ら、超伝導体でスピン配列の制御を実現
産業技術総合研究所(産総研)と総合科学研究機構(CROSS)、ウィーン工科大学、イムラ・ジャパンは、鉄系磁性高温超伝導体「EuRbFe▽▽4▽▽As▽▽4▽▽」の超伝導とユーロピウム(Eu)の磁性が共存する状態において、磁束量子の向きと配置を操作することで、スピン配列の制御に成功した。 大規模集積量子コンピュータ向けに集積構造を考案
大規模集積量子コンピュータ向けに集積構造を考案
産業技術総合研究所(産総研)は、シリコンスピン量子ビット素子を用いた大規模集積量子コンピュータ向けの新しい集積構造を考案した。従来構造に比べ、ラビ振動(スピンの操作速度)が約10倍高速となり、製造ばらつき耐性も大幅に改善できるという。 産総研、超伝導量子アニーリングマシンを開発
産総研、超伝導量子アニーリングマシンを開発
産業技術総合研究所(産総研)は、超伝導量子アニーリングマシンの開発と動作実証に成功した。従来方式に比べ1桁少ない量子ビット数で、組み合わせ最適化問題を解くことが可能になるという。
