第16回 差動対がオペアンプに変身（1）〜能動負荷で利得を高める〜：Analog ABC（アナログ技術基礎講座）（2/3 ページ）

[美齊津摂夫，ディー・クルー・テクノロジーズ]

2つの電流源が高利得を生む

　能動負荷とは字のごとく、「能動的な負荷」です。つまり、抵抗などの受動素子ではなく、トランジスタなどの能動素子を負荷に使います。図1に能動負荷を使った差動対を示しました。これまで負荷抵抗（Rc1とRc2）だけだったのが、PNP 型トランジスタを2個使った、カレント・ミラー回路に置き換わっています。回路を構成する2つのトランジスタの電流が鏡のようにコピーされているので、カレント・ミラー回路と呼びます。アナログ回路では、ひんぱんに使いますので、別の機会に紹介したいと思います。

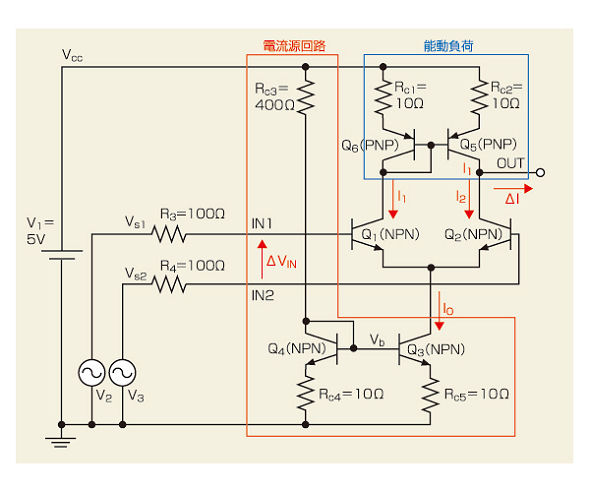図1　能動負荷を使った差動対　図中青枠で示したのが能動負荷です。能動素子であるトランジスタを2つ使ったカレント・ミラー回路と差動対を構成する2つのトランジスタの相乗効果で、利得を非常に大きな値にすることができます。

　図2に、能動負荷を使った差動対を直流解析した結果を示しました。図2（b）から電圧利得^＊1）は20×log(1.5V/100uV)= 約83.5dBと、高いことが分かると思います。なぜ利得が高くなるかと言うと、出力端子OUTにはトランジスタQ2とQ5のコレクタしか接続されていないからです。通常動作ではコレクタは電流源として動作しているので、電流が変化しない代わりに電圧はいくらでも変化します。

＊1）　電圧利得は、20log（出力電圧/入力電圧）で定義されています。

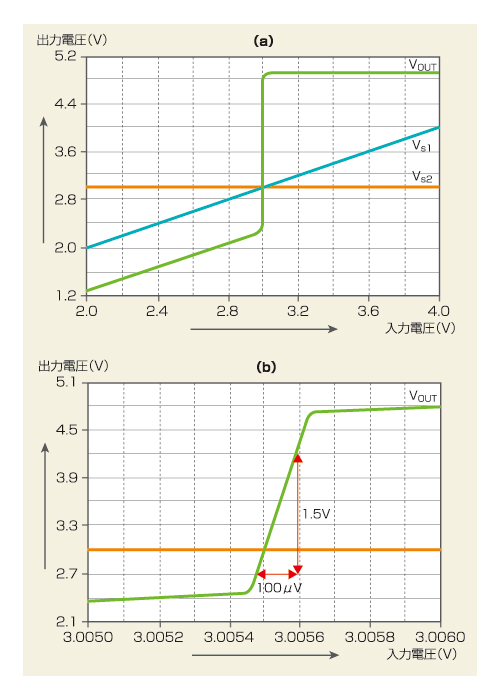図2　能動負荷を使った差動対の入出力特性　（b）は、（a）の入力電圧が3.005V 〜 3.006Vのわずかな範囲を拡大したものです。利得は入力 電圧の変化幅に対する出力電圧の変化幅ですので、（b）を見ると、利得は20×log(1.5V/100μV)=約83.5dBとなります。非常に大きな 値であることが分かります。

　図1を見て下さい。Q2（NPN型）の吸い込み電流とQ5（PNP）の吐出し電流が少しでもずれると、ずれた電流の行き場所がないので電圧は上か下に大きく動いて電流の行き場所を探し、行けるところまで行ってしまいます^＊2）。

　もう少し具体的に説明します。入力電圧VS1とVS2がちょっとずれると、Q5（PNP）とQ2（NPN）の電流がほんの少しずれます。例えば、Q1の入力電圧VS1のほうがVS2より少しだけ大きく（ΔVin）なると、Q1のコレクタ電流I1がわずかに増え、Q2のコレクタ電流I2はわずかに減ります。

　ところが、Q1のコレクタ電流I1はカレント・ミラー回路によって、トランジスタQ5(PNP)から吐出し電流I1としてそのまま出てくるので、トランジスタQ5の吐出し電流I1はQ2の吸込み電流I2よりも少しだけ多いことになります。このちょっとだけ多い分の吐出し電流は、トランジスタQ2が吸込んでくれないので（次段には流れ出ないと仮定します）、どこにも行きようがなくなってしまいます。

　そうなると、トランジスタQ2は少しでも多くの電流を吸込もうと、エミッタ・コレクタ間電圧Vceを高くします。逆に、トランジスタQ5は吐出す電流を少しでも減らそうとVceを小さくします。この結果、出力電圧は高いほうに行けるところまで行ってしまいます。

　入力電流に差があると、出力電圧は行き着くところまで行ってしまう…。つまり、わずかな電流差が非常に大きな電圧を生み出すので、電流源どうしを接続する能動負荷は、非常に高い利得を得られる回路だといえます。

＊2）　実際には、トランジスタは、飽和領域（エミッタ・コレクタ間電圧Vceが小さくなり、所定の電流が流れなくなる領域）に入って止まります。この領域ではトランジスタの応答速度が急減に遅くなります。この領域でのトランジスタの動作はシミュレーションに現れないことが多いので、実際の回路では飽和領域に入らないようにショットキ・バリア・ダイオードをつけるなどの対策が必要です。