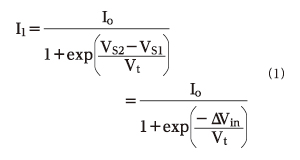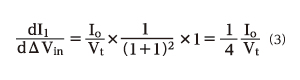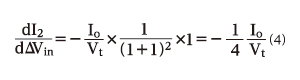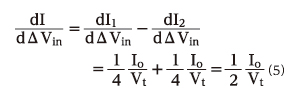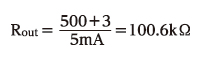第16回 差動対がオペアンプに変身（1）〜能動負荷で利得を高める〜：Analog ABC（アナログ技術基礎講座）（3/3 ページ）

[美齊津摂夫，ディー・クルー・テクノロジーズ]

アーリー電圧は大きいほど理想的

　それでは数式を使って、能動負荷を使った差動対の利得を求めてみましょう。本連載の第13回、第14回、第15回でこれまで紹介してきたように、差動対は入力信号の差分に応じて動作することが特徴です。具体的には、入力信号の差分ΔVinとトランジスタQ1のコレクタ電流I1の関係は、下記の通りです。

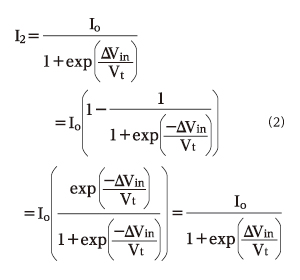
なお、トランジスタQ2のコレクタ電流I2は、合計電流がIoなので以下のように計算できます。

　I1とI2それぞれの利得の最大値は、下記のようになります。

　能動負荷はカレント・ミラーですので、I1と同じ電流がトランジスタQ5（PNP）から吐出され、出力される電流は、トランジスタQ2のコレクタ電流I2との差分になります。従って、その利得は以下のようになります。

　（5）式だけを見ると前回に紹介した固定抵抗を負荷に使ったときの利得の2倍にしかならないように見えますが、実は負荷抵抗が大きく違うのです。前回の負荷抵抗は100Ωですが、能動負荷を使った今回は、理想的には無限大です。無限大の負荷抵抗が付いているので利得は無限大となるはずなのですが、実際にはコレクタは理想的な電流源ではありません。非常に大きな値ではありますが、出力インピーダンスがあり、これが負荷抵抗となるので利得は有限の値になります。

　トランジスタのコレクタが理想的な電流源に近いかどうかを示すパラメータが「アーリー電圧（Early Voltage）」です。この値が大きくなればなるほど、コレクタは理想的な電流源となります。アーリー電圧の定義を、図3に示しました。トランジスタのVce−Ic特性において、ベース電流をパラメータにしたグラフのうち、Icが立ち上がった後ほぼ一定に推移している部分を左に伸ばしていくと、ひとつの電圧で交差します。この電圧が、アーリー電圧です。図3では分かりやすいようにアーリー電圧Vafが10Vのときをシミュレーション結果として示しました。実際には、数10 〜数100Vが標準的な値です。

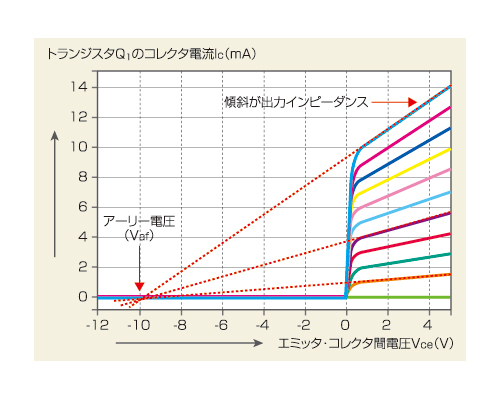図3　トランジスタのアーリー電圧を求めるグラフ　エミッタ・コレクタ間電圧Vceとコレクタ電流Icの関係を、ベース電流をパラメータとして示しました。Icが平らになっている部分を左に伸ばしていくと、ひとつの電圧（−10V）で交差します。この電圧がアーリー電圧で、この値が大きくなればなるほど、コレクタは理想的な電流源となります。

　今回シミュレーションに使ったトランジスタのアーリー電圧は500Vです。このトランジスタにVce=3Vで5mAのバイアスをかけているときの出力インピーダンス（すなわち負荷抵抗）Routは、

となります。（5）式から利得を計算すると

となり、図2のシミュレーションとほぼ一致します。次回は、能動負荷を使った差動対の応答速度を、交流解析の結果をまじえながら考察しましょう。アンプの応答速度を考察する上で、信号源のインピーダンス（図1のR3とR4）が非常に重要です。

今回はこの信号源インピーダンスを考慮していませんでしたので、次回は考慮した上で再度シミュレーションします。

→「Analog ABC（アナログ技術基礎講座）」連載一覧←

Profile

美齊津摂夫（みさいず せつお）

1986年に大手の通信系ハードウエア開発会社に入社し、光通信向けモジュールの開発に携わる。2004年に、ディー・クルー・テクノロジーズに入社。現在は、同社の常務取締役CTO（最高技術責任者）兼プラットフォーム開発統括部長を務めている。「大学では電気工学科に所属していたのですが、学生のときにはアナログ回路の勉強を避けていました。ですから、トランジスタや電界効果トランジスタ（FET）を使ったアナログ回路の世界には、社会人になってから出会ったといっていいと思います。なぜかアナログ回路の魅力に取りつかれ、23年目になりました」（同氏）。