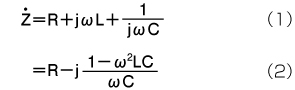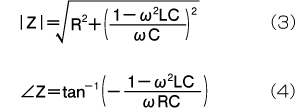第3回 回路はすべてオームの法則から(後編):Analog ABC(アナログ技術基礎講座)(2/2 ページ)
共振時のZの不思議
共振時のインピーダンスZが、ゼロになったり、インダクタやコンデンサそのものの値を超えて無限大になったりするのを不思議に感じるかもしれません。そこで、簡単な絵を使って、感覚的な説明をしたいと思います。
図2(a)を見て下さい。直列回路の共振時は、インダクタとコンデンサが接続されている点(図中の黒い点)の電圧が上下に共振周波数で振動します。この振動に伴って、流れる電流値(図中の赤の矢印)が変わりますがインダクタとコンデンサに印加する電圧の合計値(図中の青い破線)は変化しません。電流の変化量に比べて電圧の変化量が小さいことは、オームの法則によってインピーダンスが低いことを意味し、電圧がまったく変化しないとき、インピーダンスはゼロになります。
一方、並列回路の共振時の様子を図2(b)に示しました。共振時は、インダクタとコンデンサの両方の電圧が上下に共振周波数で振動します。このとき、インダクタとコンデンサは互いに同じ量のエネルギをやりとりします。つまり、電流はインダクタとコンデンサを周回するだけで、外部には出てきません。電圧の変化量に対して、電流に変化量が小さいことは、インピーダンスが大きいことを意味します。電圧が変化しても電流がまったく流れなかったら、そのときのインピーダンスは無限大になります。
前回紹介したインピーダンスの計算式を使って、実際に直列回路の共振周波数を算出してみましょう。図1(a)に示した直列回路のインピーダンスZは、次の式で表せます。
実部と虚部が得られれば、直列回路のインピーダンスの大きさ|Z|と、位相角∠Zを計算できます。
式(3)と式(4)、オームの法則を使えば、電圧と電流の大きさや、それらの周波数に対する変化といった各種特性が計算できます。ここでは、虚部がゼロ、すなわち「1−ω2LC=0」になる場合に注目しましょう。このとき周波数fを、角周波数ω=2πfの関係から計算すると以下のようになります。
このとき、インダクタのインピーダンスXLはjωL=j√(L/C)、コンデンサのインピーダンスXCは、1/jωC=−j√(L/C)となり、大きさ(絶対値)が等しくなります。回路全体のインピーダンスは(3)式からZ=Rになります。R=0ならば、Z=0になることが数式からも分かります。式(5)で示した周波数が共振周波数です。
次回からは、アナログ回路を構成する重要な回路を1つずつ紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか

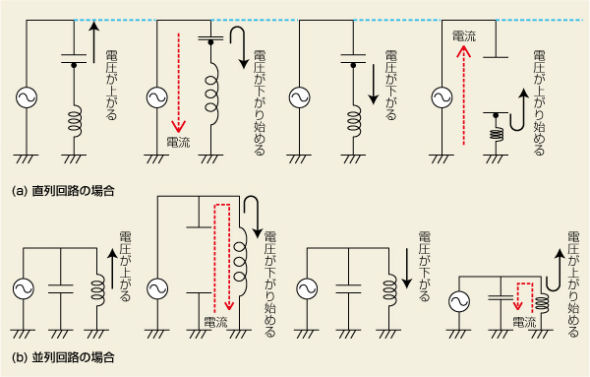 図2 共振現象の「感覚的」な説明 共振時のインピーダンスZは、直列回路ではゼロに近づき(a)、一方、並列回路では無限大に近づきます(b)。
図2 共振現象の「感覚的」な説明 共振時のインピーダンスZは、直列回路ではゼロに近づき(a)、一方、並列回路では無限大に近づきます(b)。