誘電体の比誘電率（k）は、一定とは限らない：福田昭のストレージ通信（61） 強誘電体メモリの再発見（5）（1/2 ページ）

外部電界の強さと分極の大きさの関係は、強誘電体を含めた誘電体全体ではどうなっているのだろうか。「ヒステリシス・ループ」を使って解説していこう。

[福田昭，EE Times Japan]

外部電界と分極の関係を整理する

　前回は、強誘電体（ferroelectric materials）に加える外部電界を変化させたとき、強誘電体の分極（polarization）がどのように変化していくかをエネルギーポテンシャルと電流の変化を含めて説明した。それでは、外部電界の強さと分極の大きさの関係は、強誘電体を含めた誘電体（dielectric materials）全体ではどうなっているのだろうか。

　本連載の第3回で、分極の大きさは「外部電界の強さ（E）」および「比誘電率（k）マイナス1」に比例すると述べた。このことを数式で表現すると、

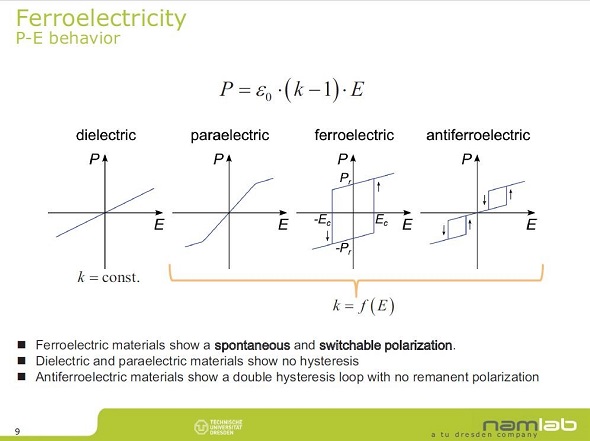
　分極（P）＝真空中の誘電率（ε0）×（（比誘電率（k）−1）×（外部電界（E））

となる。ここで分極（P）を縦軸（Y軸）、外部電界（E）を横軸（X軸）とするグラフを描き、両者の関係を表現してみよう。

　真空中の誘電率（ε0）は常に一定である。留意すべきなのは、比誘電率（k）が「必ずしも一定ではない」ことだ。一部の誘電体は、外部電界（E）がかなり強くなると比誘電率（k）が小さくなる。このためグラフは折れ線あるいは曲線となり、分極（P）は飽和傾向を示す。いずれも外部電界（E）がゼロになると、分極（P）もゼロに戻る。

　また本稿では、外部電界（E）が静電界あるいは非常にゆっくりと変化する電界である場合を想定している。外部電界（E）が素早く変化したり、あるいは高い周波数の交流電界であったりすると、比誘電率（k）は大きく変化する。高周波電界は、ここでは考慮しない。

強誘電体の「ヒステリシス・ループ」

　強誘電体の比誘電率（k）に関しては主に、以下の3つの特徴がある。比誘電率（k）が外部電界（E）によって大きく変化すること、外部電界（E）がゼロになっても分極（P）が残ること、外部電界（E）の変化の仕方（履歴）によって分極（P）が異なること。これら3つの特徴は、「ヒステリシス・カーブ」（あるいは「ヒステリシス・ループ」）と呼ばれる、強誘電体に特有の曲線を分極（P）-外部電界（E）関係のグラフで描かれる。

　ヒステリシス・ループの出発点はどこでも良いのだが、本稿では、外部電界（E）がゼロの地点からスタートする。このとき、強誘電体にはプラスの分極が残っているとする（残留分極（Pr））。ここでマイナス方向の外部電界をゼロから少しずつ強めていくと、分極が下がり始める。始めはほとんど下がらないが、あるところからは、急激に分極が減少する。そしてマイナスの外部電界がある強さ（抗電界）に達すると、分極がゼロになる。

　マイナスの外部電界をさらに少しだけ強めると、分極はマイナスになり、マイナスの分極が急激に増加する。さらに電界を強めると、あるところからは分極はほとんど増えなくなり、ほぼ飽和する。

　そこでマイナスの外部電界を弱めてゼロにする。するとマイナスの分極は最大から少し下がったところで残る（残留分極）。

　ここからプラスの外部電界を加える。ゼロから少しずつ電界を強めていくと、始めは分極は少しだけ減っていき、ある電界値（抗電界）で急激に減少し、ゼロになる。さらに電界を強めていくと分極はプラスに反転し、急激に増加する。そして一定の値で飽和する。

　分極が飽和傾向にあることを確認してからプラスの外部電界を弱めていき、ゼロにする。分極は最大値から少し下がったところに残る（残留分極）。これで出発点に戻ったことになる。

　なお、上記のようなヒステリシス・カーブは理想的な強誘電体の場合だ。実際に製造した強誘電体の薄膜（強誘電体メモリでは薄膜を利用する）では、ヒステリシス・カーブは理想から外れた、ゆがんだものになることが珍しくない。

誘電体の種類と、分極（P）-外部電界（E）の関係を示すグラフ。左から誘電体、常誘電体、強誘電体、反強誘電体。出典：NaMLabおよびドレスデン工科大学（クリックで拡大）