理研ら、機械学習法で「量子スピン液体」を解明:制限ボルツマンマシンを採用
理化学研究所(理研)らの共同研究チームは、機械学習を用いて「量子スピン液体」を解明した。スーパーコンピュータ「富岳」などを活用して大規模計算を行い実現した。
大規模計算にスパコン「富岳」や「京」などを活用
理化学研究所(理研)創発物性科学研究センター計算物質科学研究チームの野村悠祐研究員と、豊田理化学研究所/早稲田大学理工学術院総合研究所の今田正俊フェロー/上級研究員・研究院教授による共同研究チームは2021年8月、機械学習を用いて「量子スピン液体」を解明したと発表した。スーパーコンピュータ「富岳」などを活用した大規模計算により実現した。
絶対零度でもスピンの向きがゆらぐ「電子スピン液体」の状態では、スピンが分裂したような「スピノン」と呼ばれる励起が生じるといわれている。一般的な磁性体のスピン励起とは異なる量子もつれの特性を持つため、量子コンピュータにおける量子計算に有用だと考えられている。ただ、「量子スピン液体相が実際に存在するのか」「どのような性質のスピン液体なのか」といった議論については、物理の分野でまだ決着がついていないという。
研究チームは今回、膨大なスピン配置パターンの重ね合わせによって表現される量子もつれの本質的なパターンを見つけ出すため、機械学習技術を用いることにした。具体的には、人工ニューラルネットワークの一種である確率生成モデル「制限ボルツマンマシン」を採用した。物理分野で使われる関数を用い、重要な量子もつれをあらかじめ取り込むなど、機械学習の能力を高める工夫もした。
高度な量子もつれを学習するには、学習用データとしてさまざまなスピン配置パターンを生成する必要がある。このような大規模計算を、東京大学物性研究所のスーパーコンピュータと理研のスーパーコンピュータ「京」および「富岳」で実施した。その結果、高い精度で量子スピン間のもつれを捉えることに成功したという。
この手法を、2次元正方格子上のJ1-J2量子ハイゼンベルグ模型に適用した。正方形が敷き詰められた格子上の各点に量子スピンが存在し、これらが最近接スピン間の相互作用J1と、次近接スピン間の相互作用J2によって相互作用し合う。J1とJ2の相互作用はそれぞれ、「ネール型」と「ストライプ型」のスピン配置を好み、競合するという。計算結果により、強く量子もつれをしている量子スピン液体は、J2/J1=0.5付近で実現することが分かった。
異なる相の境界を決める場合、高い精度を得る方法として「絶対零度の状態から決める方法」と「励起状態の構造から決める方法」の2種類がある。これらは相補的で、今回はこの2つの相図決定手法による結果が一致したという。
また、量子スピン液体状態における励起構造も調べた。計算で求めたスピンの励起構造は、対称性の高い波数で励起エネルギーがゼロとなり、その周りで円すい状に線形分散を持つことが分かった。これは、スピンが分裂してスピノン励起が形成され、それらもディラック型の線形分散を持つという描像と整合した。これらの結果は、量子スピン液体において、分数化した励起が独立した粒子のように振る舞う、特別な励起構造であることを示すものだという。
 2次元正方格子上におけるJ1-J2ハイゼンベルグ模型の量子スピン液体相における励起構造。左は計算で求めたスピンの励起構造概念図、右はその背後に隠れたスピノン励起が予想される励起エネルギーの構造概念図 出典:理研
2次元正方格子上におけるJ1-J2ハイゼンベルグ模型の量子スピン液体相における励起構造。左は計算で求めたスピンの励起構造概念図、右はその背後に隠れたスピノン励起が予想される励起エネルギーの構造概念図 出典:理研今回の研究成果について研究チームは、「量子スピン液体を現実の物質で実現するための有用な指針になる。量子スピン液体相において発現すると考えられる『スピノン』というスピンが分裂した特殊な粒子は、量子コンピューティングにおける量子計算への応用が期待できる」とみている。
関連記事
 単純立方格子状に3次元自己集合した超結晶を作製
単純立方格子状に3次元自己集合した超結晶を作製
理化学研究所(理研)創発物性科学研究センター創発超分子材料研究チームは、硫化鉛(PbS)のコロイド量子ドットをゲル浸透クロマトグラフィー(GPC)処理することで、配位子密度が制御できることを明らかにし、単純立方格子状に3次元自己集合した超結晶の作製に成功した。 理研、高移動度で低電圧駆動の有機半導体材料発見
理研、高移動度で低電圧駆動の有機半導体材料発見
理化学研究所(理研)は、キャリア移動度が30cm2/Vs超と極めて高く、低電圧で駆動する有機半導体材料を発見したと発表した。ディスプレイやIDタグなどへの応用が期待される。 スパコン「富岳」が3期連続で4冠達成
スパコン「富岳」が3期連続で4冠達成
富士通は2021年6月29日、同社と理化学研究所(理研)が共同開発したスーパーコンピュータ(スパコン)「富岳」が、世界のスパコン関連ランキングにおいて、「TOP500」「HPCG(High Performance Conjugate Gradient)」「HPL-AI」「Graph500」の全てのベンチマークにおいて第1位を獲得したと発表した。 理研、3量子ビットもつれ状態の生成に成功
理研、3量子ビットもつれ状態の生成に成功
理化学研究所(理研)は、シリコン量子ドットデバイスでは初めて、3量子ビットもつれ状態を生成することに成功した。大規模量子コンピュータの開発に弾みをつける。 第一原理計算で結晶の性質を解析する手法を開発
第一原理計算で結晶の性質を解析する手法を開発
理化学研究所(理研)と大阪大学の共同研究チームは、ニューラルネットワークを用いて、固体結晶の電子状態に関する第一原理計算を、精密に行うことができる新たな手法を開発した。 理研ら、新たな「スピン流−電流変換現象」を発見
理研ら、新たな「スピン流−電流変換現象」を発見
理化学研究所(理研)らによる国際共同研究グループは、独自に開発した数値シミュレーション法を用い、スピン流を電流の渦に変換する、新たな「スピン流−電流変換現象」を発見した。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか

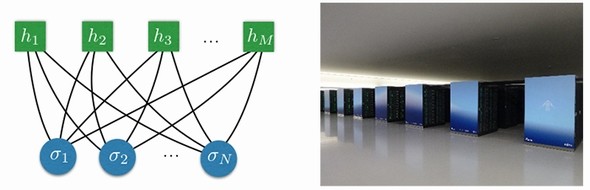 左は「制限ボルツマンマシン」の構造概念図、右はスーパーコンピュータ「富岳」の外観 出典:理研
左は「制限ボルツマンマシン」の構造概念図、右はスーパーコンピュータ「富岳」の外観 出典:理研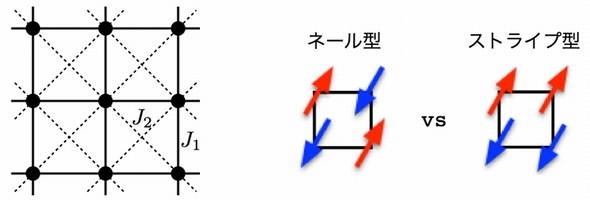
 上図は2次元正方格子上のJ1-J2ハイゼンベルグ模型とそのスピン配置の競合。下図は2次元正方格子上のJ1-J2ハイゼンベルグ模型の絶対零度相図 出典:理研
上図は2次元正方格子上のJ1-J2ハイゼンベルグ模型とそのスピン配置の競合。下図は2次元正方格子上のJ1-J2ハイゼンベルグ模型の絶対零度相図 出典:理研