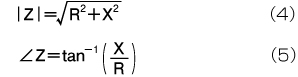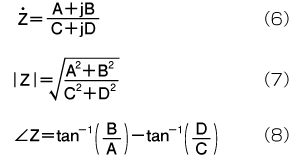第2回 回路はすべてオームの法則から(前編):Analog ABC(アナログ技術基礎講座)(2/2 ページ)
電圧が先か、電流が先か
詳しく説明しましょう。このオームの法則は、「抵抗の両端に電圧をかける(印加する)と抵抗に電流が流れ、逆に抵抗に電流を流すと抵抗の両端には電圧が発生する」という現象を表現しているにすぎません。しかし、この現象はどのような電子回路でも発生します。線形増幅器や非線形なデジタル回路、直流動作のレギュレータ回路、高周波(RF)回路であろうと一緒です。抵抗の両端に電圧がかかれば電流が流れ、抵抗に電流が流れれば電圧が発生するのです。
以上のように説明をすると、読者の皆さんは「電流と電圧はどちらが先に発生しているのか」と疑問に思うかもしれません。この疑問に答えるために、前述の電圧源(V)と電流源(I)という2つの電源について説明します。オームの法則を説明するときに一度、電圧を表すのに「V」という記号を使っているので混乱するかもしれませんが、電圧源と電圧では意味が大きく違います。
電圧源は、「電圧の源」なので文字の並びからは、電圧がいくらでもわき出てきそうな印象を受けます。実際はそうではありません。どんなに電圧を変えようとしても、ガンとして電圧が変わらないのが電圧源なのです。その代わりに、いくらでも電流が流れます。一方の電流源は、電圧源の逆の動作をします。誰がなんと言おうと、電流源ごとに決まった値の電流を流します。その代わり、どのような電圧になってもお構いなしで、電圧は変わります。すなわち、電圧源を使って抵抗に電圧を印加すると、オームの法則に従って、電流が流れます。電流源を使って抵抗に電流を流すと、オームの法則に従って、電圧が発生するのです。
この現象は、どのような複雑な電子回路でも同じです。オームの法則から外れたような挙動は起きていませんし、起こすこともできません。
「R」から「Z」へ
オームの法則は、扱う信号が「直流」の場合だけでなく、「交流」の場合でも成り立ちます。そもそも直流とは、時間に対して電圧値や電流値が変化しないことを意味します。一方、交流では、時間に対して振幅や位相が変化します。電子回路に入力する信号は多くの場合、交流信号です。例えば、電波やインターネット回線を流れる信号、音声信号、センサーから取得する温度信号などは交流です。
式(1)と(2)を見たときに、「抵抗しかないけれども、3種類の素子のうちコンデンサとインダクタはどこにあるの」と疑問に思ったかもしれません。コンデンサやインダクタは、交流信号の周波数によって抵抗値が変わる素子と考えられるので、基本的には抵抗と同じように扱えばよいのです。交流信号を扱う場合には、純粋な抵抗成分Rではなく、周波数に対して変化する抵抗値を示すインピーダンス「Z」を、Rの代わりに使います。純粋な抵抗成分だけで電子回路を表現できるのは、扱う信号が直流の場合だけなのです。
「jω」が登場
インピーダンスZは、一般に次のように表せます(Zの上に付けた「・」は、複素形式であることを示します)。
Rを実部、jが付いているXを虚部と呼びます。インダクタのインピーダンスXLはjωL、コンデンサのインピーダンスXCは1/jωCで、それぞれ理想的には純抵抗成分(実部)がありません。
このようにインピーダンスを表す式には、虚数単位である「j」と、角周波数「ω」という2つの記号が頻繁に出てきます。ω=2πf(fは交流信号の周波数)という関係があり、ωが計算式に入っていることは周波数fによって抵抗値などの特性が変わることを示します。また、複素数表現を使うことで、「大きさ(絶対値)」と「位相角」を同時に表します。位相角とは、入力信号に対して出力信号がどれだけの時間ずれるかという情報です。
インピーダンスZの大きさ(抵抗値)|Z|と位相角∠Zは、それぞれ次のように計算できます。
3種類の素子(抵抗、コンデンサ、インダクタ)についても、すべて式(4)と式(5)に当てはめることができます。このほか、インピーダンスZを次の(6)式のように表現した場合の|Z|と∠Zを計算する、式(7)と(8)は覚えておくと便利です。
次回は、簡単な回路を例に挙げ、今回紹介した計算式を使ってインピーダンスを求め、その回路に現われる現象を調べてみます。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか