NVIDIAが解説するディープラーニングの基礎(前編):歴史から仕組み、学習まで(3/4 ページ)
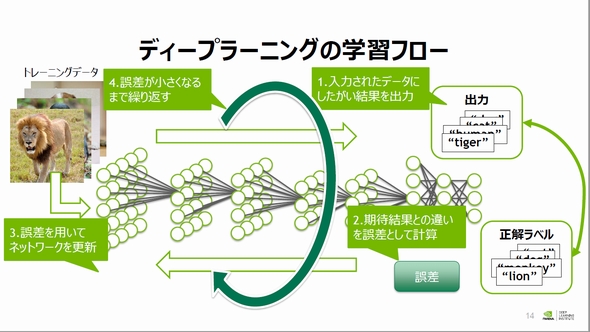
ディープラーニングの学習フロー
学習プロセスでは、期待結果とネットワークの誤った出力の差を誤差として定量的に計算すること、誤差から各層の重み係数を更新することがカギとなる。
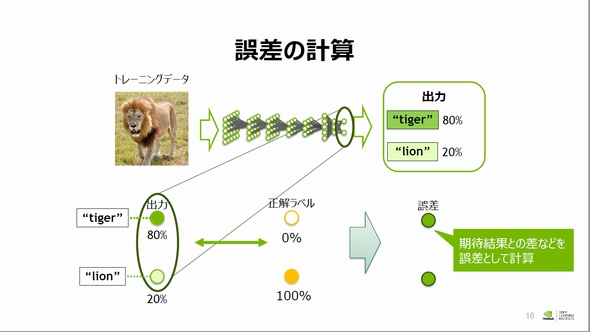
山崎氏は画像分類をテーマとして、誤差計算のイメージを例示した。この例ではネットワークにライオンの画像を入力したにもかかわらず、トラの確率スコアが80%、ライオンの確率スコアが20%と出力され、誤ってトラと分類されている。
誤差計算について、山崎氏は「問題設定により誤差はいろいろ定義できるが、(この例では)出力された確率スコアと数値化した正解ラベルの直接的な差分を用いる」ことなどが基本的な考え方だと説明した。
勾配法と誤差逆伝播法でネットワークの重み係数を更新
得られた誤差から各層の重み係数を更新する手法についてもいくつか提案されているが、山崎氏は「最もベースとなる考え方の『勾配法』を紹介する」とした。
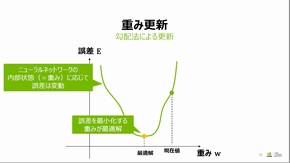
ニューラルネットワークは各層の重み係数によって内部状態が変化するため、重み係数に応じて誤差は変動することになる。よって、誤差を最小化する重み係数を探索する必要がある。
山崎氏は、問題の簡単化のため1次元空間上に重み係数と誤差の関数を例示した。このような関数で誤差を最小化する重み係数の最適解を探索するためには、任意の区間での重み係数で誤差の傾き(勾配)を算出し、この傾きの正負により重み係数を増減させることで誤差の傾きが0となる重み係数の探索を行う。これが勾配法のイメージとなる。
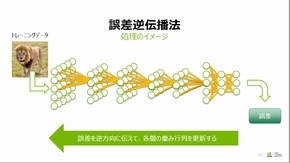
また、ニューラルネットワークの学習には全ての層で重み係数の最適解を更新する必要がある。しかし、ある層の重み係数最適解を直接計算することは困難であり、「誤差逆伝播法」を用いることで各層の重み係数を更新する。
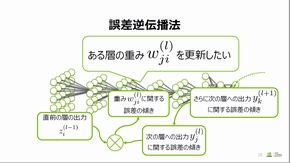
誤差逆伝播法では、ある層の重み係数に関する誤差の傾きを直前層の出力と直後層の出力に関する誤差の傾きによって計算する。ここで、直後層の出力に関する誤差の傾きはその次層の出力に関する誤差の傾きで算出できるため、誤差が通常のネットワークの流れと異なり、出力層から入力層へ向けて伝播することから誤差逆伝播法と名付けられたという。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング