ダイオードを使った整流回路の解析:複数のダイオードをカスケード接続した回路:福田昭のデバイス通信(365) imecが語るワイヤレス電力伝送技術(19)(1/2 ページ)
ダイオードを使った整流回路の解析について、複数のダイオードを接続した整流回路兼電圧逓倍回路を解説する。
(ご注意)今回は前回の続きとなっています。まず前回の内容を読まれることを推奨します。
複数のダイオードとコンデンサによって整流と逓倍を実現
前回は、ダイオードを使った整流器(整流回路)を解析する4つの手法の中で、常微分方程式を数値計算によって解く手法と、EDA(Electronic Design Automation)ソフトウェアを使う手法を簡単に説明した。今回は、ダイオードをカスケード接続した回路を使う手法をご紹介する。
 ダイオードを使った整流回路の主な解析手法。今回は4番目の手法を扱う[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)
ダイオードを使った整流回路の主な解析手法。今回は4番目の手法を扱う[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)複数のダイオードをカスケード接続し、前段のダイオードのアノード側と後段のダイオードのカソード側をコンデンサで結んだ回路を想定する。交流を直流に整流する回路であるとともに、交流電圧を逓倍する回路となる。このような回路は「ビラード・カスケード電圧逓倍回路(Villard cascade voltage multiplier)」、あるいは「コッククロフト・ウォルトン電圧逓倍回路(Cockcroft-Walton voltage multiplier)」などと呼ばれる。
整流逓倍回路の基本動作
4個のダイオードと4個のコンデンサで構成する整流逓倍回路を考えよう。交流(あるいは高周波)入力に対し、コンデンサは短絡回路と見なせる。このため、4個のダイオードによる入力インピーダンスZinは4分の1となる。N個のダイオードとN個のコンデンサで同様の回路を構成したときは、入力インピーダンスはZin/Nに減少する。
直流入力に対し、コンデンサは開放回路と見なせる。従って入力電圧V0は4倍に増加する(厳密にはコンデンサへの充電を繰り返すことで電圧が倍増する)。N個のダイオードとN個のコンデンサで同様の回路を構成したときは、出力電圧はV0のN倍に増える。
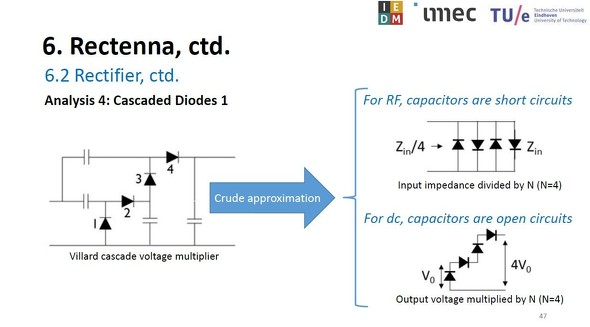 ダイオードをカスケード接続した回路の例(ビラード・カスケード電圧逓倍回路あるいはコッククロフト・ウォルトン電圧逓倍回路)とそのふるまい[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)
ダイオードをカスケード接続した回路の例(ビラード・カスケード電圧逓倍回路あるいはコッククロフト・ウォルトン電圧逓倍回路)とそのふるまい[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)ビラード・カスケード電圧逓倍回路を利用した解析方法は2つ選んだ。1つは「Ritz-Galerkin(リッツ・ガラーキン)法」を当てはめる方法、もう1つは「常微分方程式(ODE:Ordinary Differential Equation)」を当てはめる方法である。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- 2026年半導体市場の3大トピックを深掘り ―― DRAM不足の真相とTSMC、Intelの逆襲
- NANDを再定義、HBMを補完するAI用メモリ技術「HBF」
- 2nm世代以降のGAAチップの性能向上へ、AMATの新装置
- IntelがTowerとの製造契約撤回を表明
- インターポーザに複数のシリコンダイを近接して並べる2.5次元集積化
- WD、2029年に100TB HDD実現へ 「SSDとの差」縮小も狙う
- NORフラッシュにもAI需要の波、迫る供給危機
- TELが掲げる「半導体製造のDX」 最大の課題は何か
- ルネサスがGFと協業、米国での半導体製造を加速
- SiCのスイッチング損失28%削減! 東芝の新ゲートドライバー技術
