ダイオードを使った整流回路の解析:複数のダイオードをカスケード接続した回路:福田昭のデバイス通信(365) imecが語るワイヤレス電力伝送技術(19)(2/2 ページ)
» 2022年06月02日 11時30分 公開
[福田昭,EE Times Japan]
ビラード整流逓倍回路をリッツ・ガラーキン法に当てはめる
「Ritz-Galerkin(リッツ・ガラーキン)法」による近似解法は本シリーズの第17回(前々回)で説明した。ビラード・カスケード電圧逓倍回路のダイオード数をNとすると、第17回で説明した入力の高周波電力Pavと出力の直流電圧Vdcの関係式は以下のように変化する。すなわち高周波電源の寄生抵抗RgはNRgに増加し、負荷抵抗のRLはRL/Nに減少する。
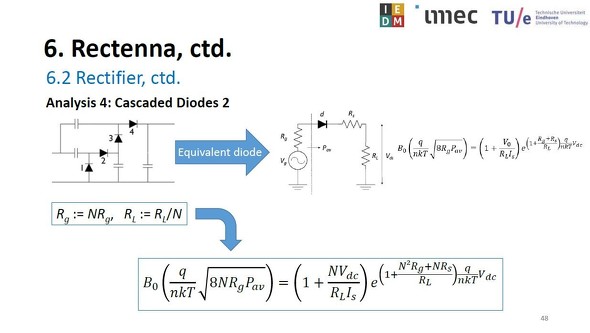 「Ritz-Galerkin(リッツ・ガラーキン)法」にビラード・カスケード電圧逓倍回路を当てはめる。入力と出力の関係式はダイオードの数Nによって変化する[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)
「Ritz-Galerkin(リッツ・ガラーキン)法」にビラード・カスケード電圧逓倍回路を当てはめる。入力と出力の関係式はダイオードの数Nによって変化する[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)ビラード・カスケード電圧逓倍回路のダイオード数を2個とした場合と、4個とした場合でリッツ・ガラーキン法による近似解と測定値を比較した。負荷抵抗を100Ωから100kΩまで3桁ほど変化させ、入力電力と出力電圧の関係を求めた。近似解と測定値はかなり良く一致した。ダイオードの数による違いはあまり見られなかった。
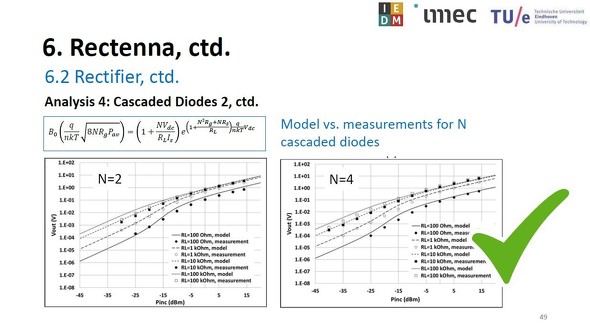 整流回路の入力電力(横軸)と出力電圧(縦軸)の関係(近似解と測定値)。左はカスケード接続したダイオードを2個(N=2)、右はダイオードを4個(N=4)とした場合[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)
整流回路の入力電力(横軸)と出力電圧(縦軸)の関係(近似解と測定値)。左はカスケード接続したダイオードを2個(N=2)、右はダイオードを4個(N=4)とした場合[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)入力インピーダンスを常微分方程式から計算する
次に、ダイオードの数がn個(n段)の ビラード・カスケード電圧逓倍回路(整流逓倍回路)の入力インピーダンスZrectifier,n-stagesを求めることを考えよう。具体的には、1個のダイオードによる整流回路の等価回路モデルを常微分方程式で表現し、入力インピーダンス(抵抗成分Rとリアクタンス成分X)を計算する。
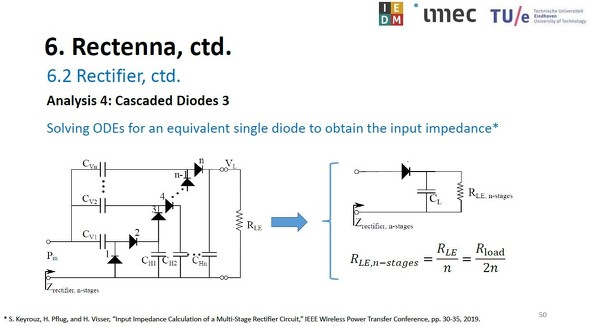 ダイオードの数がn個(n段)のビラード・カスケード電圧逓倍回路(整流回路)(左)と、1個のダイオードでまとめた等価回路(右)[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)
ダイオードの数がn個(n段)のビラード・カスケード電圧逓倍回路(整流回路)(左)と、1個のダイオードでまとめた等価回路(右)[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)ダイオードの数を2個、4個、6個と変更して計算した結果は以下のようになった。抵抗成分の大きさはダイオードの数に依存しない。周波数が増加すると抵抗成分が急激に減少する特性も、ダイオードの数によらず等しい。
リアクタンス成分の大きさはダイオードの数によって大きく変化する。周波数特性はダイオードの数によらない。周波数が増加するとリアクタンス成分は減少する。
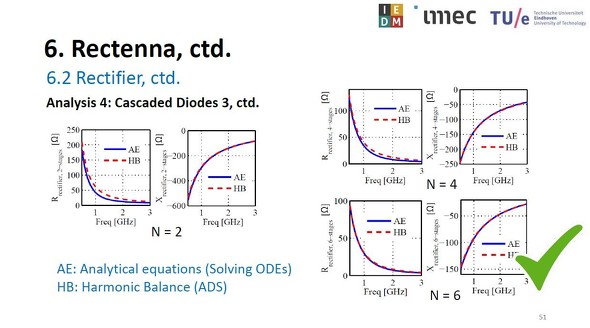 入力インピーダンスの抵抗成分Rとリアクタンス成分Xの計算結果。左はダイオードが2個の場合。右上はダイオードが4個、右下はダイオードが6個の場合。AEは常微分方程式を解いた結果。HBはEDAソフトウェア「ADS」による解析結果[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)
入力インピーダンスの抵抗成分Rとリアクタンス成分Xの計算結果。左はダイオードが2個の場合。右上はダイオードが4個、右下はダイオードが6個の場合。AEは常微分方程式を解いた結果。HBはEDAソフトウェア「ADS」による解析結果[クリックで拡大] 出所:imecおよびEindhoven University of Technology(IEDMショートコースの講演「Practical Implementation of Wireless Power Transfer」のスライドから)⇒「福田昭のデバイス通信」連載バックナンバー一覧
関連記事
 ワイヤレス電力伝送の過去から未来までを展望
ワイヤレス電力伝送の過去から未来までを展望
今回から、「IEDM 2021」でオランダimec Holst Centreでシニアリサーチャー、オランダEindhoven University of TechnologyでフルプロフェッサーをつとめるHubregt J. Visser氏が講演した「Practical Implementation of Wireless Power Transfer(ワイヤレス電力伝送の実用的な実装)」の内容を紹介する。 大電力対応ワイヤレス充電用シート型コイルを開発
大電力対応ワイヤレス充電用シート型コイルを開発
大日本印刷(DNP)は、電動車や無人搬送車(AGV)向けに、11.1kWクラスの大電力伝送に対応しつつ、薄型軽量でコスト低減を可能にした「ワイヤレス充電用シート型コイル」を開発した。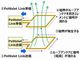 数ミリ〜数十センチ間で、数百Mbpsの高速無線通信
数ミリ〜数十センチ間で、数百Mbpsの高速無線通信
パナソニックは2021年11月10日、OFDM(直交周波数分割多重)変調方式の一つであるWavelet OFDMを適用した近距離無線通信技術「PaWalet Link」を開発したと発表した。 GaNベースの無線充電器、出力は最大300WでEVにも
GaNベースの無線充電器、出力は最大300WでEVにも
ワイヤレス充電器などを手掛けるイタリアのスタートアップEggtronicが特許権を有するACワイヤレス給電技術「E2WATT」は、ホーム/自動車アプリケーションなどに向けたワイヤレス充電の電力効率を向上させることが可能だという。 シリコンフォトニクスとは何か
シリコンフォトニクスとは何か
今回は、「シリコンフォトニクス」技術を紹介する。そもそも「シリコンフォトニクス」とは何か、そしてその利点と課題について解説したい。 シリコンフォトニクスの技術開発ロードマップ
シリコンフォトニクスの技術開発ロードマップ
今回は、シリコンフォトニクスの技術開発ロードマップを解説する。シリコンフォトニクスの性能向上とコストを、16/14nmから5nm、3nmの技術ノードに沿って見ていこう。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
記事ランキング
Special SitePR
あなたにおすすめの記事PR
