高周波の非線形特性を高精度に解析、新概念の「Xパラメータ」で実現:無線通信技術(3/5 ページ)
基本波のみ入力時のパラメータ表現
非線形素子の出力信号Bは、入力信号Aの関数として次の式で表せる。
AとBいずれについても、2つの添え字のうち1つ目(i)はポートの番号で、2つ目(j)は高調波の次数を示す。例えば、B23はポート2の出力信号の3次高調波、A11はポート1の入力信号の基本波(1次)、A12はポート1の入力信号の2次高調波を意味する。
それでは、非線形状態における素子の振る舞いを見ていこう。まず図3のように、被測定物である素子のポート1に、素子を非線形状態にするのに十分な電力の信号(ドライブ・トーン)を入力する。すると出力には、ドライブ・トーンと同じ周波数の成分(基本波)と、ドライブ・トーンに対する高次高調波成分を含んだ信号が現れる。このとき、これらの高次高調波成分の大きさは、ドライブ・トーンの大きさによって決まる。ある大きさのドライブ・トーンに対して、どの程度の大きさの高次高調波成分が発生するかという関係を表現するのが式(1)中のF項(Fij)である。
付加的な高調波も考慮する
ただし、式(1)で表現できる非線形の振る舞いは、あくまでも理想的な状態である。実際には、付加的な高調波が入力される場合があるからだ。例えば前段のアンプから高次高調波成分を含んだ信号がポート1に入力されたり、それとは反対に、被測定物である素子そのものが生成した高次高調波が、負荷側のインピーダンス不整合によってポート2に反射してきたりする場合がある。
こうした信号が存在する場合、非線形素子の入出力信号は、図4(a)に示すような状態になる。すなわち、ポート1の入力はドライブ・トーンに前段が出力した高次高調波が重畳されたものになり、ポート2の入力は負荷側のインピーダンス不整合による反射信号になる。出力には、これら基本波と高調波の相互関係によって生成された成分が現れる。そこで、こうした状態もパラメータ表現できるように式(1)を拡張する必要がある。
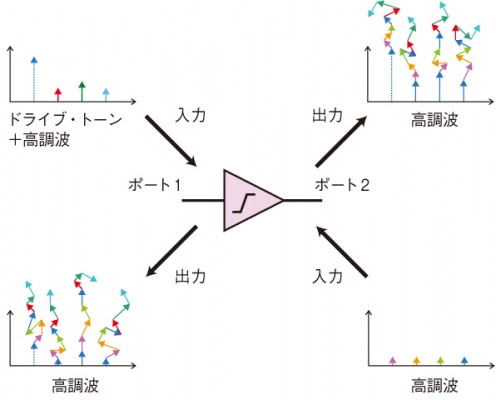 図4(a) 非線形素子に基本波と高調波を入力 非線形素子に、ドライブ・トーン(基本波)のほか、小信号の高調波が印加された場合のイメージである。出力には、ドライブ・トーンによって素子の内部で生成された高調波と、外部から印加された高調波成分とが合成された信号が現れる。
図4(a) 非線形素子に基本波と高調波を入力 非線形素子に、ドライブ・トーン(基本波)のほか、小信号の高調波が印加された場合のイメージである。出力には、ドライブ・トーンによって素子の内部で生成された高調波と、外部から印加された高調波成分とが合成された信号が現れる。このとき素子の各ポートにおける出力信号は、ドライブ・トーン自体の周波数とドライブ・トーンによって素子内部で生じる高次高調波成分、外部から入力されるドライブ・トーン相当の周波数と高次高調波成分との合成によって決まる。ここで重要な点は、基本波と高次高調波によって、同じ周波数の信号成分が2つ生成されるということである。図4(b)を見てほしい。
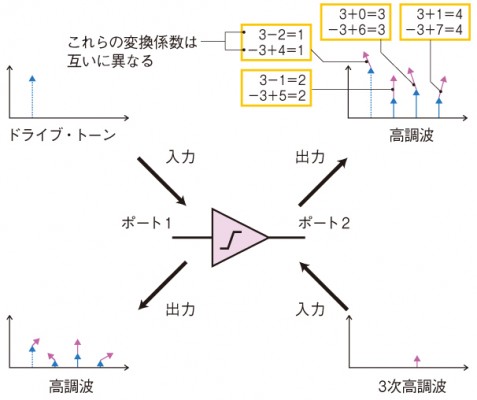 図4(b) 非線形素子に基本波と高調波を入力 非線形素子に、ドライブ・トーン(基本波)のほか、小信号の高調波が印加された場合のイメージである。出力に現れた合成信号は、周波数が同じでも実際には2つの成分からなる。例えば、ポート2に出力される2次高調波は、1つはドライブ・トーンと外部印加の3次高調波との混合によるもので、もう1つはドライブ・トーンによって素子内部で発生した5次高調波と外部印加の3次高調波との混合によるものである。
図4(b) 非線形素子に基本波と高調波を入力 非線形素子に、ドライブ・トーン(基本波)のほか、小信号の高調波が印加された場合のイメージである。出力に現れた合成信号は、周波数が同じでも実際には2つの成分からなる。例えば、ポート2に出力される2次高調波は、1つはドライブ・トーンと外部印加の3次高調波との混合によるもので、もう1つはドライブ・トーンによって素子内部で発生した5次高調波と外部印加の3次高調波との混合によるものである。例えば、ドライブ・トーンによって非線形状態に維持された素子に3次高調波を入力した場合を考えてみる。この場合、出力の2次高調波成分は2つあり、1つ目はポート1から入力された基本波(ドライブ・トーン)とポート2から入力された3次高調波の混合によって生じる2次高調波成分で、2つ目はポート1から入力された基本波によって素子の内部で生成される5次高調波と、ポート2から入力された3次高調波との混合によって生じる2次高調波成分である。
出力に現れるこれら2つの成分は、入力との関係がそれぞれ異なっている。従って、これらをパラメータで表現するとき、それぞれに異なる係数が必要になる。その際に、複素共役を取り入れることで、これら2つの係数を簡単に表現できる(図4(c))。これら2つの係数をS項、T項とする。
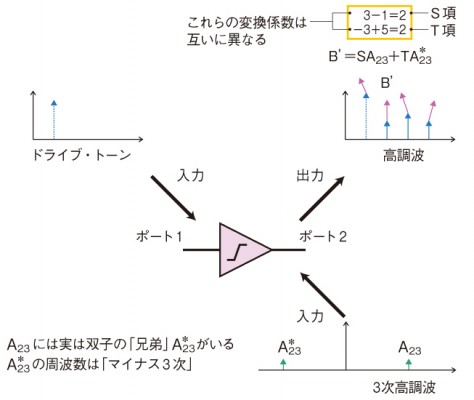 図4(c) 非線形素子に基本波と高調波を入力 非線形素子に、ドライブ・トーン(基本波)のほか、小信号の高調波が印加された場合のイメージである。出力に現れた合成信号は、周波数が同じでも実際には2つの成分からなり、それら2つの成分をパラメータ表現するには、それぞれに異なる係数を導入する必要がある。これらの係数をS項、T項とする。
図4(c) 非線形素子に基本波と高調波を入力 非線形素子に、ドライブ・トーン(基本波)のほか、小信号の高調波が印加された場合のイメージである。出力に現れた合成信号は、周波数が同じでも実際には2つの成分からなり、それら2つの成分をパラメータ表現するには、それぞれに異なる係数を導入する必要がある。これらの係数をS項、T項とする。例えば、ポート2の出力の2次高調波成分のうち、ポート2の入力の3次高調波成分による寄与分は、B’ = SA23+TA*23という形で表せる。つまり、素子に入力される小信号である3次高調波の正負の周波数成分(A23とA*23)に、別々の係数であるSとTがそれぞれ掛かっているわけだ。
先に説明したF項に加えて、S項とT項を導入すると、非線形素子の入出力関係は次の式で表現できる。F項と同様に、S項、T項もドライブ・トーンの電力に対する依存性を有することに注意してほしい。
ただし、P=A11/|A11|である。|A11|は素子に入力されるドライブ・トーン(ポート1に印加される基本波)の振幅を示す。このほか、各添え字の意味は以下の通りである。
i:出力信号のポート番号(i = 1,2,3…)
j:出力信号の高調波次数(j = 1,2,3…)
k:入力信号のポート番号(k = 1,2,3…)
l:入力信号の高調波次数(l = 1,2,3…)
この式(2)を使えば、基本波から高調波まで含んだ情報をパラメータ表現することが可能になる。この式(2)で使われているF項、S項、T項がXパラメータである。
高調波にも重ねの理を適用できる
式(2)において、F項のみならずS項とT項についても、全次数の成分の加算(重ね合わせ)で表現できることに注目してほしい。この理由は、高調波は小信号であるため線形と見なすことができ、重ね合わせの理を適用できるからである。
一般に、非線形領域における素子は大信号の下で動作しており、重ね合わせの理は適用できない。しかし、非線形領域も微小な区間に分ければ、個々の区間については線形領域と見なせる。このことから、非線形動作の素子についても、例えばパワー・アンプの入力側ポートに狭帯域の信号を印加した状態のように、基本波の大信号入力(A11)が支配的で、そのほかのすべての入力信号(高調波成分)は比較的小さいという場合は、入出力の関係に重ね合わせの理を適用できることが分かる†1)。図5は、簡略化してA1とB2のみを示した例である。
線形領域ではSパラメータと等価
線形動作つまり小信号動作の場合、ドライブ・トーンの振幅である|A11|は小さい。このため、高調波成分は発生せず、周波数の混合も起きないため、T項は無視できる。また、S項(X(S))のうち、周波数を相互に関係付ける項もゼロになる。これより式(2)は次のように表せる。
ここで基本波(j=1、l=1のとき)だけを考慮すれば、高調波の表記は不要となるため、式(4)が得られる。
理解しやすくするため、対象の素子を2ポートと仮定しよう。すなわち、i=1、2でk=2の場合である。実際に式(4)のiとkにこれらの数字を当てはめると、次のようになる。
ここでは|A11|が小さい、線形領域の動作を考えているため、非線形性を示すF項(X(F))をパラメータ表現に用いる必要はない。つまりF項に関してはSパラメータと同様に考えることができ、従ってX(F)i1はSi1と等価になる。またS項(X(S))については、前述の通り周波数相互を関係付ける項がゼロになることから、i=1、2の場合にそれぞれ線形のSパラメータのS12、S22と等価になる。よって、式(5)は以下の式(6)で表せる。
先に定義した通りP=A11/|A11|なので、次のように変形できる。
ここで、A11はポート1から入力される基本波を表しており、これは線形素子のパラメータ表現におけるa1と等価だと分かる。同様にA21はポート2から入力される基本波を表しており、a2と等価だ。出力信号であるB11、B21についても、同様に線形素子のパラメータ表現におけるb1、b2と等価だと分かる。従って、式(7)は最終的に以下のようになる。
これは、2ポートのSパラメータの表記そのものである。このことから、Xパラメータで表現した式(2)は、線形のSパラメータで表現した式を非線形に拡張したものだといえる。
ビヘイビア・モデルとして利用する
これまでに説明した通り、Xパラメータは非線形素子の入出力における基本波と高次高調波の関係をパラメータ表現している。このパラメータの情報を使えば、非線形回路の振る舞いをコンピュータ上でシミュレーションするためのビヘイビア・モデルを作成できる。これを「PHD(Poly Harmonic Distortion)モデル」と呼ぶ†2)。
2ポート素子を例に取り、ポート2の出力(B2)の生成メカニズムを図示すると図6になる。ここでは簡略化して、入力信号(A1とA2)と出力信号(B2)のみを考え、発生する高調波は3次までを考慮した。
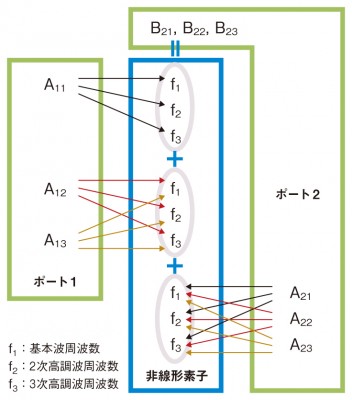 図6 PHDモデルの概念 Xパラメータのデータに基づく非線形素子のシミュレーション・モデル「PHDモデル」の概念である。ポート1とポート2において、3次高調波までを考慮し、入力信号(A1、A2)と出力信号(B2)の関係を示す。A、Bの添え字は、順にポート番号、高調波次数を示す。例えば、A11はポート1の基本波、A21はポート2の基本波、A22はポート2の2次高調波、A23はポート2の3次高調波である。
図6 PHDモデルの概念 Xパラメータのデータに基づく非線形素子のシミュレーション・モデル「PHDモデル」の概念である。ポート1とポート2において、3次高調波までを考慮し、入力信号(A1、A2)と出力信号(B2)の関係を示す。A、Bの添え字は、順にポート番号、高調波次数を示す。例えば、A11はポート1の基本波、A21はポート2の基本波、A22はポート2の2次高調波、A23はポート2の3次高調波である。ドライブ・トーンの基本波(A11)が入力されたとき、出力信号(B2)には非線形性によって素子内部で発生した高調波(f1、f2、f3)が含まれる。しかもこれらの高調波成分はそれぞれが、前段からポート1に入力されるドライブ・トーンの高調波成分であるA12、A13や、インピーダンス不整合によってポート2に入射する高調波成分であるA21、A22、A23の影響を受ける。従って、この影響は図6に示すようにマトリクス状になる。
図6や式(2)で示したように、非線形素子に入出力する信号の関連性を表現するのが、PHDモデルの概念である。
電子ファイルでシミュレータに渡す
ベクトル・ネットワーク・アナライザによる測定で得たXパラメータは、テキスト形式の電子ファイルとして保存できる。SパラメータをTouchStone形式やCitifile形式などさまざまなファイル形式で記録し、シミュレータにデータとして読み込んでモデルを作成できるのと同様に、Xパラメータのデータも電子ファイルを介してシミュレータに渡す。
この電子ファイル中には、図7のようにデータが格納されている。Xパラメータのデータは、基本波の周波数や場合によってはDCバイアスなどの条件ごとのブロックに分かれており、各ブロックの中には、基本波の信号レベルを変えたときのXパラメータのF項、S項、T項が記述されている。
 図7 Xパラメータの電子ファイル ベクトル・ネットワーク・アナライザに基づく測定器で測定したXパラメータを電子ファイルに保存した例である。測定範囲内の各周波数ポイントにおいて、基本波の信号レベルごとにXパラメータのF項、S項、T項の値が格納されている。
図7 Xパラメータの電子ファイル ベクトル・ネットワーク・アナライザに基づく測定器で測定したXパラメータを電子ファイルに保存した例である。測定範囲内の各周波数ポイントにおいて、基本波の信号レベルごとにXパラメータのF項、S項、T項の値が格納されている。図7の例では、基本波の周波数は5GHzで、ドライブ・トーンのレベルを0.029から順次変えたときの各信号レベルでのXパラメータが記述されている。ここで、S項やT項のラベルに付いている数字は、Sパラメータと同様のポート番号のほか、Xパラメータ独自の基本波・高次高調波の次数の値である。一例を示すと「T_2_3_1_3」は「T23,13」を意味しており、ポート1から入力された3次高調波とポート2から出力された3次高調波との関係を表すT項を指す。
実際には、高周波回路を開発するエンジニアが、このデータを直接考察することはない。通常はこのデータを当社の高周波回路向け設計ツール「ADS(Advanced Design System)」に読み込んでPHDモデルを生成し、シミュレーションを実行することで初めて意味のある考察が可能になる。ADS上ではXパラメータから生成したPHDモデルは1つの部品として扱われ、画面上では図8のように表示される。
次ページ以降は、Xパラメータの実際の作成方法と活用方法について解説する。
参考文献
†1)J. Verspecht and P. Van Esch, “Accurately characterizing hard nonlinear behavior of microwave components with the nonlinear network measurement system: Introducing ‘nonlinear scattering functions,’” in Proc. 5th Int. Workshop Integrated Nonlinear Microwave Millimeterwave Circuits, Germany, Oct. 1998, pp. 17-26.
†2)Jan Verspecht and David E. Root, Polyharmonic Distortion Modeling, 2006 IEEE microwave magazine, June 2006.
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- 村田製作所は増収減益、米Resonantのれん438億円減損
- IDT買収から7年、ルネサスがタイミング事業をSiTimeに売却

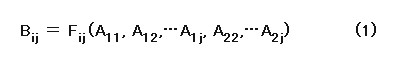
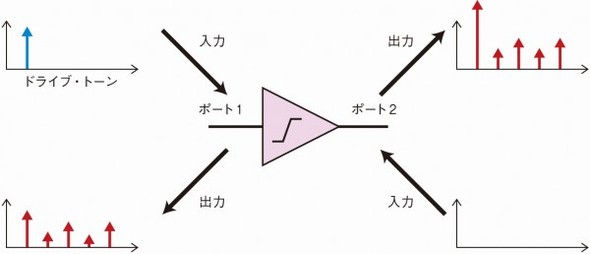 図3 非線形素子に基本波を入力 非線形素子に、ドライブ・トーンとして基本波のみを入力した場合のイメージである。基本波の高調波成分が出力に現れる。
図3 非線形素子に基本波を入力 非線形素子に、ドライブ・トーンとして基本波のみを入力した場合のイメージである。基本波の高調波成分が出力に現れる。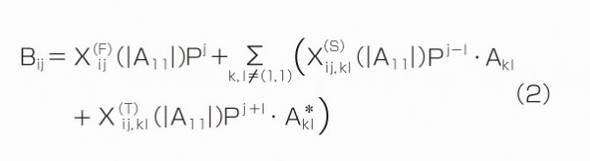
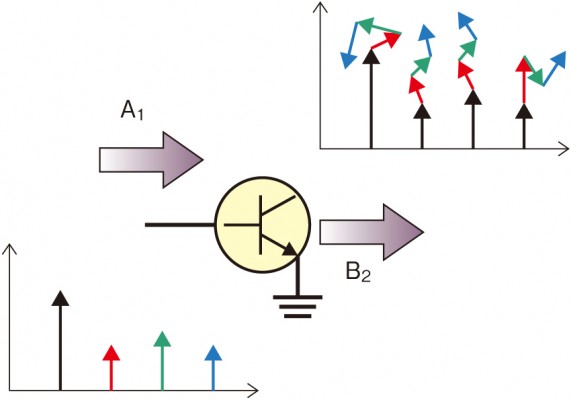 図5 非線形領域でも重ねの理が成り立つ 非線形領域においても、小信号に着目すれば重ね合わせの理が成り立つ。
図5 非線形領域でも重ねの理が成り立つ 非線形領域においても、小信号に着目すれば重ね合わせの理が成り立つ。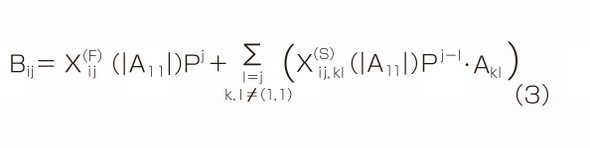
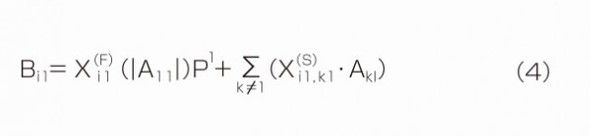
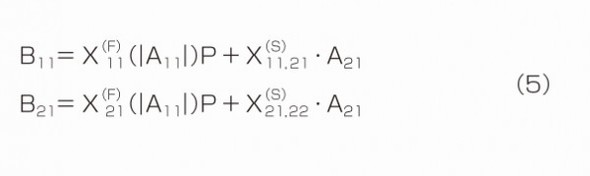

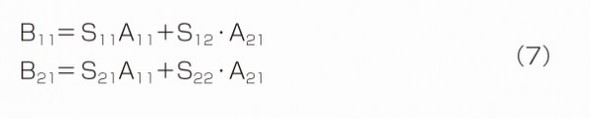

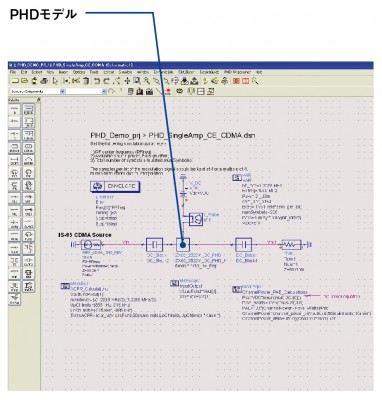 図8 PHDモデルを使ったシミュレーション 高周波回路向け設計ツール「ADS(Advanced Design System)」にXパラメータの電子ファイルを読み込んで作成したPHDモデルの例である。
図8 PHDモデルを使ったシミュレーション 高周波回路向け設計ツール「ADS(Advanced Design System)」にXパラメータの電子ファイルを読み込んで作成したPHDモデルの例である。