高周波の非線形特性を高精度に解析、新概念の「Xパラメータ」で実現:無線通信技術(5/5 ページ)
Xパラメータの活用方法
続いて、Xパラメータの高周波回路シミュレータ上での活用方法について解説しよう。
本稿の前半で述べた通り、非線形ベクトル・ネットワーク・アナライザで測定したXパラメータのデータを電子ファイル化して出力し、当社の高周波回路設計ツール「ADS(Advanced Design System)」に読み込むことで、回路シミュレーションのモデルとして利用できる。
ADS上では、やはり本稿の前半で説明した通り、Xパラメータから「PHD(Poly-Harmonic-Distortion)モデル」を生成し、シミュレーションに用いる。PHDモデル生成のためには、「デザイン・キット」と呼ぶADSのアドオン・モジュールが必要である。デザイン・キットをインストールすると、図3に示したメニューを利用できるようになる。所定のフォルダにXパラメータの電子ファイルを置いておき、このメニューから、例えば「Create All PHD Components(PHDモデル作成)」を選択するとPHDモデルが生成され、モデル・ライブラリに登録される。後は、回路図エディタ上でモデル・ライブラリからこのPHDモデルを呼び出し、信号源モデルや周辺回路モデルを組み合わせて回路全体を構築してから、シミュレーションを実行すればよい。非線形特性を高い精度で予測できる。
非線形シミュレーションの実例
Xパラメータに基づくPHDモデルを利用した非線形特性解析の実際を、具体例を挙げて説明しよう。入力振幅に対する出力振幅の非線形性(AM-AM特性)や、入力振幅に対する出力位相の非線形性(AM-PM特性)、隣接チャネル漏えい電力比(ACPR:Adjacent Channel Power Ratio)を解析可能だ。
具体的な事例として、利得が23.5dB、最大出力レベルが18dBmの市販アンプを被測定物としてXパラメータを求めて、ADSで特性を評価した結果を紹介する。
図4は、実際の回路を測定して得られたXパラメータをPHDモデル化し、ハーモニック・バランス解析*1)を実行した結果である。基本波、2次高調波、3次高調波にAM-AM特性やAM-PM特性が現れていることが読み取れる。例えば、基本波において、入力レベルを増加させたとき出力レベル特性(AM-AM特性)は、約−10dBm入力から出力が飽和し始めているのが分かる。同様に、入力レベルを増加させたときの出力の位相特性(AM-PM特性)は、入力レベルの増加に伴って変化しているのが見てとれる。AM-AM特性やAM-PM特性によるこうした歪みは、無線信号の品質を劣化させる要因になる。
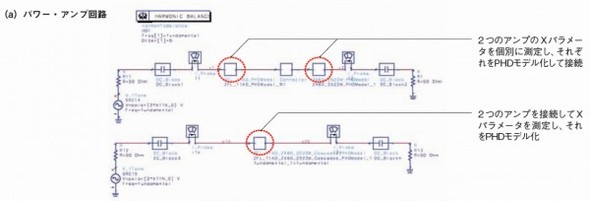
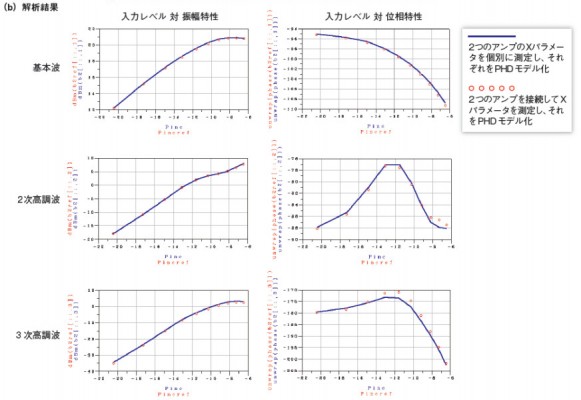 図4 ハーモニック・バランス解析の結果 (a)は解析対象の回路である。利得が11dB、最大出力レベルが3dBmの市販アンプと、利得が23.5dB、最大出力レベルが18dBmの市販アンプをカスケード(従続)接続した。上側の回路は、2つのアンプのXパラメータを個別に測定し、それぞれを基にPHDモデルを作成してから、PDHモデル同士を接続したもの。これに対し下側の回路は、2つのアンプを接続した状態でXパラメータを測定し、それを基にPHDモデルを作成した。(b)はハーモニック・バランス解析の結果である。(a)に示した2つの回路について、基本波と2次高調波、3次高調波それぞれの入力レベル 対 振幅特性と入力レベル 対 位相特性を解析した。
図4 ハーモニック・バランス解析の結果 (a)は解析対象の回路である。利得が11dB、最大出力レベルが3dBmの市販アンプと、利得が23.5dB、最大出力レベルが18dBmの市販アンプをカスケード(従続)接続した。上側の回路は、2つのアンプのXパラメータを個別に測定し、それぞれを基にPHDモデルを作成してから、PDHモデル同士を接続したもの。これに対し下側の回路は、2つのアンプを接続した状態でXパラメータを測定し、それを基にPHDモデルを作成した。(b)はハーモニック・バランス解析の結果である。(a)に示した2つの回路について、基本波と2次高調波、3次高調波それぞれの入力レベル 対 振幅特性と入力レベル 対 位相特性を解析した。図5は、サーキット・エンベロープ解析*2)によって隣接チャネル漏えい電力比を解析した結果である。アンプの入出力間でこの特性がどの程度悪化しているかを評価できる。
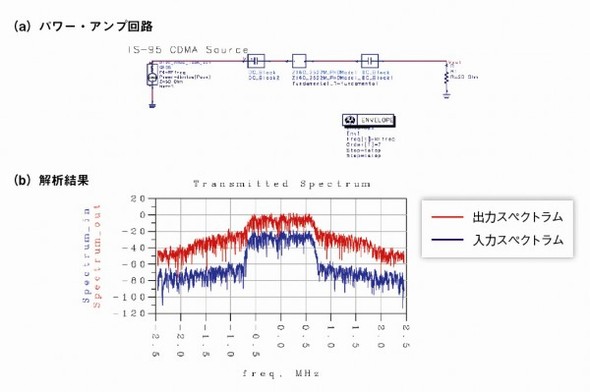 図5 サーキット・エンベロープ解析の結果 (a)は解析対象の回路である。図4の市販アンプ(利得は23.5dB、最大出力レベルは18dBm)のPHDモデルを使った。(b)はサーキット・エンベロープ解析で隣接チャネル漏えい電力比を解析した結果である。
図5 サーキット・エンベロープ解析の結果 (a)は解析対象の回路である。図4の市販アンプ(利得は23.5dB、最大出力レベルは18dBm)のPHDモデルを使った。(b)はサーキット・エンベロープ解析で隣接チャネル漏えい電力比を解析した結果である。利害得失を把握してモデルを使い分ける
高周波回路シミュレータのADSでは、ビヘイビア・モデルとしたXパラメータに基づくPHDモデルのほか、従来から「AmplifierS2D」や「AmplifierP2D」などが利用できた。各モデルには利害得失があり、解析の目的に応じて適切に使い分けるべきである。そこで表1に、各ビヘイビア・モデルの比較を示した。比較項目としては、「非線形特性」と「負荷インピーダンス依存性」、「バイアス依存性」、「雑音」、「測定器の対応」の5項目を挙げた。
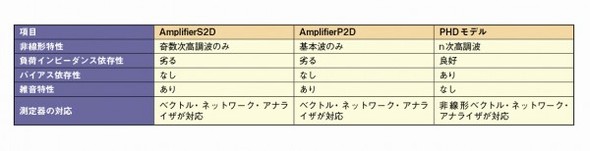 表1 高周波シミュレーション用ビヘイビア・モデルの利害得失 高周波回路シミュレータのADSで利用できる各種ビヘイビア・モデルには、それぞれ利害得失がある。この表では、各種ビヘイビア・モデルを「非線形特性」と「負荷インピーダンス依存性」、「バイアス依存性」、「雑音」、「測定器の対応」の5項目で比較した。
表1 高周波シミュレーション用ビヘイビア・モデルの利害得失 高周波回路シミュレータのADSで利用できる各種ビヘイビア・モデルには、それぞれ利害得失がある。この表では、各種ビヘイビア・モデルを「非線形特性」と「負荷インピーダンス依存性」、「バイアス依存性」、「雑音」、「測定器の対応」の5項目で比較した。非線形特性
ここで非線形特性とは、どのような次数の高調波を表現できるかである。
実際の高周波回路では、奇数次高調波や偶数次高調波が生じる可能性がある。ところがAmplifierS2Dに出力が歪むような大信号を入力するシミュレーションを実行しても、出力には奇数次高調波しか現れない。同様に、AmplifierP2Dでは基本波しか出力されない。つまりこれらのビヘイビア・モデルは、高調波を評価するシミュレーションには向いていない。
これに対しXパラメータに基づくPHDモデルは、シミュレーション上、奇数次と偶数次の高調波を表現できる。従って、AM-AM特性やAM-PM特性などを高い精度で予測可能である。
負荷インピーダンス依存性
回路の出力側に接続された負荷が変化したとき、回路特性が変化する度合いのことである。
実際の高周波回路ではこうした特性変化が生じるが、AmplifierS2DとAmplifierP2Dではいずれもそれを表現することが難しい。これは、複数のビヘイビア・モデルを組み合わせて構成したシステムを解析する際に誤差の要因になってしまう。ビヘイビア・モデルを複数個カスケード(従続)接続した際に、段間のインピーダンス不整合を考慮できないからだ。この場合、隣接チャネル漏えい電力比の解析において結果に最大2dBの誤差が生じることが実際に報告されている†1)。
これに対しPHDモデルでは、複数のPHDモデルをカスケード接続した際に、段間のインピーダンス不整合も考慮される。しかも、非線形ベクトル・ネットワーク・アナライザを利用して、負荷インピーダンスを変化させながらXパラメータを測定するロードプル測定システムも用意されており、そのXパラメータを基に作成したPHDモデルは、負荷インピーダンスの広い範囲で良好な特性を示す。
バイアス依存性
電源電圧など、回路に与えるバイアス条件が変化した際に、回路の特性が変化する度合いを表す特性である。
AmplifierS2DとAmplifierP2Dは、いずれもモデルとしてバイアス・ポートを備えていないため、バイアス条件を変化させた際の特性への影響を解析するシミュレーションには対応できない。
これに対しPHDモデルは、信号の入出力ポートに加えて、電源電圧ポートを付加できるため、パワー・アンプなどの電力付加効率(PAE:Power Added Efficiency)をシミュレーションできる。
雑音特性
雑音特性をモデルとして表現できるかどうかである。
AmplifierS2DとAmplifierP2Dはともに、雑音指数や等価雑音抵抗などのパラメータを備えており、これらを設定することで雑音特性を考慮したシミュレーションが可能である。例えば、アンプのビヘイビア・モデルに雑音特性が与えられていれば、アンプを通過した信号がアンプの雑音指数によってどの程度劣化するかをシミュレーションで評価できる。
一方でPHDモデルは、こうした特性をモデルとして表現することはできない。これがPHDモデルをシミュレーションに使う上での制約になる。
測定器の対応
ビヘイビア・モデルの基になるデータを測定器が自動的に作成できるかどうかである。
AmplifierS2DとAmplifierP2Dは、一般的なベクトル・ネットワーク・アナライザを使って得た測定値から作成できる。PHDモデルも、Xパラメータの測定データから作成するが、すでに説明した通り既存のネットワーク・アナライザではXパラメータの測定に対応できない。非線形ベクトル・ネットワーク・アナライザが必要になる。
応用範囲がさらに広がる
非線形ベクトル・ネットワーク・アナライザは通常、一般的なベクトル・ネットワーク・アナライザと同様に50Ω系で測定を行う。すなわち測定ポートは50Ωで校正されており、被測定物から見た負荷インピーダンスは、常に50Ωに固定されている。
ただし、実際の被測定物は入出力インピーダンスが50Ωからずれている場合があり、その測定にはインピーダンス・チューナと組み合わせたいわゆるロードプル測定システムが必要になる。
こうしたロードプル測定システムは、前項で負荷インピーダンス依存性について説明した際に触れた通り、すでに実用化されている。ベクトル・ネットワーク・アナライザ用校正キットやロードプル測定用インピーダンス・チューナ装置を手掛ける米Maury Microwave社が開発した。非線形ベクトル・ネットワーク・アナライザに、同社が開発したロードプル測定ソフトウエアを搭載して、測定ポートと被測定物の出力ポートの間に、インピーダンス・チューナ装置を挿入する。こうすれば負荷インピーダンスを変化させながら非線形特性を測定できる。
こうして取得したXパラメータを基に、ADS上でPHDモデルを作成すれば、前述の通り、負荷インピーダンス依存性がある非線形回路を高い精度で解析できる。非線形回路の評価や設計の効率を大幅に高める強力なツールになるだろう。
PHDモデルの応用範囲をさらに広げる取り組みも進めている。現在のところPHDモデルを作成するには、測定によって得られたXパラメータが必須である。そこで当社は、ADS上の回路から直接、PHDモデルを生成する機能を計画中である。これが実現されれば、PHDモデルの応用範囲が一段と広がるはずだ。
参考文献
†1)Arnaud Soury, Edouard Ngoya, Jean Rousset, “Behavioral Modeling of RF and Microwave Circuit Blocks for Hierarchical Simulation of Modern Transceivers,” IEEE/MTT-S IMS Digest, pp. 975-978, June 2005.
注釈
*1)ハーモニック・バランス解析は、周波数領域のシミュレーションである。主に無変調周波 数を対象としており、変調信号など周波数が連続的に変化する信号の解析は困難である。解析手法は以下の通りである。すなわちキルヒホッフの電流則に従って、回路中の各ノードに流れ込む電流の総和がゼロとなるよう周波数ごとに電流を推測する。ここで、各ノードにおける電流の総和がゼロから離れている程度を「誤差」とし、この誤差が十分小さくなる(解が収束する)まで計算を繰り返す。収束した値がそのノードにおける定常解として得られる仕組みだ。抵抗やインダクタ、コンデンサなどの線形素子を流れる電流は周波数領域で計算するが、ダイオードやトランジスタなど非線形素子に流れる電流は時間領域で計算し、その結果を周波数領域に変換する。
*2)サーキット・エンベロープ解析は、高周波変調信号を高速にシミュレーションできるようハーモニック・バランス解析を拡張したものである。時間領域解析と周波数領域解析の両方の特徴を併せ持つ。具体的には、キャリア周波数ではなく、エンベロープ(包絡線)の時間変化をサンプリングして解析する。この各サンプルに対してハーモニック・バランス解析を次々と実行する。これにより各時間ステップでの周波数応答、言い換えると時間とともに変化するフーリエ係数が得られる。こうして得られた時間と周波数の2次元配列から、ある1つの周波数を選択して、そのエンベロープ時間変化をフーリエ変換することで、その周波数を中心としたスペクトルを得る仕組みだ。
Profile
阿部貢(あべ みつぐ)氏は現在、アジレント・テクノロジーのEEsof EDA事業部 マーケティング・サービス部門 EDAテクニカルサポート・コンサルティングで、高周波設計ツールのサポートやコンサルティングを担当している。蓑和浩(みのわ ひろし)氏は、同社の電子計測本部 マーケティングセンタ ワイヤレスビジネスユニットで、無線通信などの用途の電子部品/モジュールに向けた測定器を担当するマーケット ディベロップメント マネージャを務めている。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか

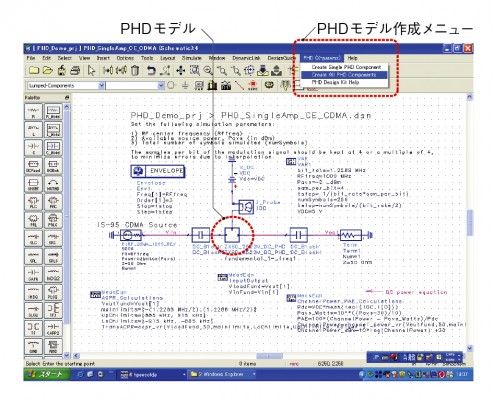 図3 シミュレータ上でPHDモデルを生成 高周波回路シミュレータ「ADS」にデザイン・キットをインストールすることで、PHDモデルの作成メニューを利用できるようになる。
図3 シミュレータ上でPHDモデルを生成 高周波回路シミュレータ「ADS」にデザイン・キットをインストールすることで、PHDモデルの作成メニューを利用できるようになる。