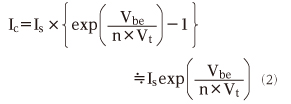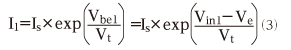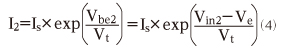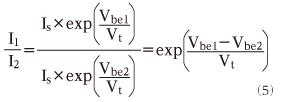第14回 差動対を手を動かして理解する:Analog ABC(アナログ技術基礎講座)(1/2 ページ)
今回は、差動対の数多くの特長や使い道のうち、同相雑音の除去機能とリミッタ機能に焦点を当てましょう。差動対がこれらの機能を備える理由を、数式をうまく使いながら紹介します。
前回は、差動対の特長を紹介しました。差動対は、1対(2つ)のトランジスタで構成した、入力信号の差分に応じて動作する回路です。例えば、振幅の制限(リミッタ)や、同相雑音の除去といった特長があるほか、コンパレータや乗算器として使えます。
今回は、差動対の数多くの特長や使い道のうち、同相雑音の除去機能とリミッタ機能に焦点を当てましょう。差動対がこれらの機能を備える理由を、数式をうまく使いながら紹介します。
数式の処理はあまり得意ではないのですが、複雑な計算式を苦労して解いた結果が、シンプルな数式に落ち着くと気持ちが良いと感じるのは筆者だけでしょうか。今回は数式の処理が主になります。手を動かしながら、数式の意味について考えてみて下さい。
入力の差電圧が出力電流比に変換
差動対の回路構成を図1に示しました。図1の右下の電流源に流れる電流をIo、トランジスタQ1のコレクタ電流をI1、トランジスタQ2のコレクタ電流をI2とします。まず、図1を見て分かるように次の関係があります。
ほかに電流が流れ出さないので当たり前の式なのですが、I1 とI2を求めるには必要な計算式です。
前述のように、差動対は入力信号の差分に応じて動作します。ですから、計算式も入力信号のVin1とVin2の差電圧に注目しながら、出力電圧のVout1とVout2を求める計算式にまとめていきます。図1から分かるように、Vout1 はI1にRc1を掛けたもの、Vout2 はI2にRc2を掛けたものですから、I1とI2を計算すれば、Vout1やVout2は簡単に分かります。
I1 とI2を計算するに当たり、トランジスタのベース-エミッタ間電圧Vbeとコレクタ電流Icの関係式を思い出して下さい。本連載の第6回で紹介した以下の計算式です。
expは「e」を底とする指数関数で、Isは飽和電流(10−15A 程度)、Vtは熱電圧(25℃で26mV程度)、nは「エミッション係数」と呼ぶ定数でここでは1にします。図1から明らかなように、I1はQ1のコレクタ電流、I2はQ2のコレクタ電流ですので、この計算式を活用できます。
それでは、(2)式を使って、I1 とI2を表してみましょう。Q1のベース電圧をVin1、Q2のベース電圧をVin2、Q1とQ2のエミッタ電圧をVeとすると、ベース-エミッタ間電圧Vbeはベース電圧Vinとエミッタ電圧Veの差(Vin1−VeまたはVin2−Ve)ですので、I1とI2はそれぞれ以下のように変形できます。
I1 とI2の比率は下記になります。
右辺に差電圧「Vbe1−Vbe2」が出てきました。差電圧が、電流の比率に変換されていることが実は、差動対の面白いところです。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか

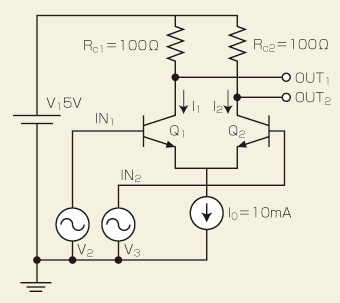 図1 幅広く使われている差動対 今回は、差動対の数多くある特長や使い道のうち、同相雑音除去効果とリミッタ効果に焦点を当てます。
図1 幅広く使われている差動対 今回は、差動対の数多くある特長や使い道のうち、同相雑音除去効果とリミッタ効果に焦点を当てます。