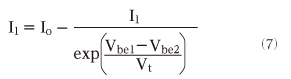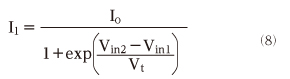第14回 差動対を手を動かして理解する：Analog ABC（アナログ技術基礎講座）（2/2 ページ）

[美齊津摂夫，ディー・クルー・テクノロジーズ]

出力電流の絶対値を求める

　電流の比率は分かったのですが、I1 とI2を求めるには、絶対値を知る必要があります。そのために、最初の（1）式が必要になります。（1）式からI1を求めると、I1=Io−I2です。I2はすでに計算した（5）式から以下のようになります。

　I1=Io−I2に（6）式を代入すると、I1の絶対値が以下のように求まります。

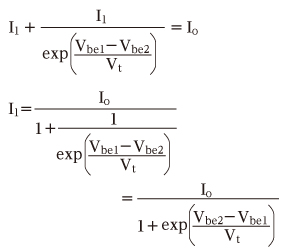
　この式をさらにI1でまとめます。

　上の式変形では、exp(1/A)＝exp（−A）という関係を使いました。Vbe1＝Vin1−Ve、Vbe2＝Vin2−Veなので、I1は以下のようになります。

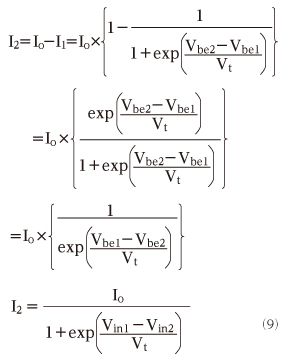
　I2についても同じように計算すると、以下のように求めることができます。

　以上の通りシンプルに、I1を表す（8）式と、I2を表す（9）式をまとめることができました。（8）式と（9）式は、指数関数expの項が逆になっているだけの簡単な式です。

差電圧で出力電流が決まる

　2つの式を見比べると、あることに気が付くと思います。I1 とI2はそれぞれ入力電圧の差（Vin1− Vin2またはVin2− Vin1）で表されているという点です。つまり、Vin1やVin2の絶対値ではなく、差電圧で決まるので同相（つまり差が一定）であれば、電流I1（またはI2）も一定になり、同相成分は出力には出てこない事になります。これが同相雑音除去の仕組みです。

分母の「exp」項の挙動が値決める

　さらに、I1 とI2の式をよくよく見比べると、リミッタ効果の仕組みも分かります。リミッタ効果とは、入力信号の振幅が大きくなりすぎたときに、出力信号（すなわち、コレクタ電流）の振幅が制限される機能でした。

　Vin2−Vin1の値が取り得る3つを例に、I1の挙動を（8）式から考えてみましょう。すなわち、（1）Vin2−Vin1がプラス無限大になった時、（2）Vin2−Vin1がゼロの時、（3）Vin2−Vin1がマイナス無限大になった時の3パターンです。

（1）I1の分母のVin2−Vin1が大きくなると、指数関数（exp）の項が無限大に近づき、これに伴ってI1はゼロになります。

（2）I1の分母のVin2−Vin1がゼロになると指数関数の項が1となって、Ioの1/2がI1に流れます。

（3）Vin2−Vin1がマイナス無限大に近づくと指数関数の項がゼロとなって、I1 はIoと等しくなり、これ以上増えません。

　以上をまとめると、I1はゼロからIoの範囲にしかならない事が分かります。I1と抵抗Rc1をかける出力電圧Vout1も規定の値以上にはならないことが分かります。Vout2も同様です。これがリミッタ効果です。

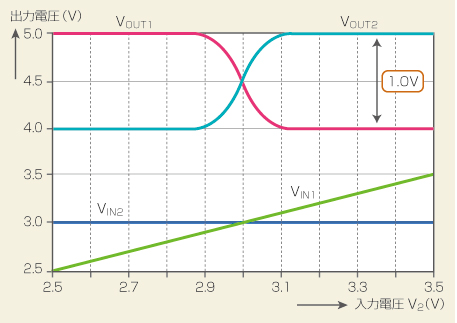図2　出力電圧差を1.0Vに制限　リミッタ効果について理解するために、入力電圧を変えたときの出力電圧の変化をグラフにしました。入力電圧Vin1（図中の緑）とVin2（図中の青）の差が大きくなり続けても、出力電圧Vout1（赤）とVout2（水色）の差は、ある一定以上には広がりません。これがリミッタ効果です。

　図1のV2（Vin1） を2.5V 〜 3.5Vに変化させたときの直流特性を図2に示しました。Io＝10mAとしていますので、I1またはI2の最大電流は10mAです。負荷抵抗Rc1とRc2はいずれも100Ωなので、出力電圧（Vout1とVout2）は10mA×100Ω=1Vでリミットが掛かります。

　差動対を実際にアンプとして使う場合には、利得と周波数特性が重要になります。次回は、今回紹介した計算式を基に、差動対の利得（増幅率）を求めましょう。周波数特性も紹介します。

→「Analog ABC（アナログ技術基礎講座）」連載一覧←

Profile

美齊津摂夫（みさいず せつお）

1986年に大手の通信系ハードウエア開発会社に入社し、光通信向けモジュールの開発に携わる。2004年に、ディー・クルー・テクノロジーズに入社。現在は、同社の常務取締役CTO（最高技術責任者）兼プラットフォーム開発統括部長を務めている。「大学では電気工学科に所属していたのですが、学生のときにはアナログ回路の勉強を避けていました。ですから、トランジスタや電界効果トランジスタ（FET）を使ったアナログ回路の世界には、社会人になってから出会ったといっていいと思います。なぜかアナログ回路の魅力に取りつかれ、23年目になりました」（同氏）。