量子コンピュータの可能性――量子テレポーテーションのパイオニア・古澤明氏に聞く：【再録】 ITmedia Virtual EXPO 2014 秋（2/5 ページ）

[EE Times Japan]

「量子もつれ」そのものが「量子コンピュータ」

EETJ　量子もつれはどのように量子コンピュータに利用できるのでしょうか。

古澤氏　量子もつれは、量子コンピュータそのものなのです。ある量子の測定の影響が、もつれている他の量子に及ぶということで、計算をしているのです。だから、それぞれの量子が“量子ゲート”になっていて、量子の測定の影響がパッパッと伝わっていくというものが計算、量子コンピュータそのものなのです。

量子テレポーテーション

EETJ　その影響が伝わる速度は光より速いのですか。

古澤氏　もちろん、もつれの影響は、ある種、光のスピードを超えているところもあるかもしれないですけれど、実際の情報として存在するためには、最終的に通信をしなければならないので、通信自体は、光や電波のスピードを超えることはありません。それは、相対性理論で、情報伝達は光速を超えないという物理の基本原理があるので、それを超えることはないです。

半加算器は2ゲート

EETJ　量子通信は、なぜ大量にデータを送れるのですか。

古澤氏　大量にというよりも、なぜ、量子コンピュータは速いのかで考えると、量子ゲートの数が圧倒的に少ないからなのです。

　計算のスピードは何で変わるかというと、ゲート数ですね。ある演算をするのに、ANDとかORとかいった論理ゲートが何個必要かということで演算のスピードが決まるわけです。このことは、量子コンピュータであろうが、古典コンピュータであろうが、一緒です。

　ゲート間の通信はもちろん、古典的な通信を行うわけで、光のスピードを超えないということは普通のコンピュータ（古典コンピュータ）と同じです。ですから、その違いは、ゲート数であり、量子コンピュータのゲート数は、指数関数的に少ないのです。

　端的に言えば、「Half adder」（半加算器）という1ビットの足し算の回路がありますが、これを論理回路、「AND」とか「OR」で作ろうとすると、7ゲート必要になります。量子コンピュータの場合は2ゲートで大丈夫です。

　計算というのは、Half adderのような回路の固まりですね。それが何万回どころか、何億回繰り返されるわけです。それが、量子コンピュータの場合、2/7で済むわけです。ですから2/7の何万、何億乗という桁で（計算速度が）変わってくるわけです。

　もっと言えば、量子力学では「重ね合わせ」の状態も使えます。古典コンピュータの場合は「0か1」ですが、量子コンピュータの場合「0と1」という重ね合わせの状態ができるので、それを何ビットも使えば、2の冪乗（べきじょう、累乗）で効いてくるわけです。それだけ、大きく一気に計算ができるので、そこも高速な理由ですね。

　ですので、整理すると、量子コンピュータが高速な理由は、2つあって、「重ね合わせの並列化ができる」のと同時に、「ゲート数が少ない」ので、圧倒的に速くなるわけです。

EETJ　量子もつれの影響はどんなに距離が離れていても及ぶのですか。

古澤氏　外から相互作用がない限り、無限に離れていてもその影響は及びます。宇宙の端から端に離れていても大丈夫で、距離は関係ありません。

「完全な量子テレポーテーション」

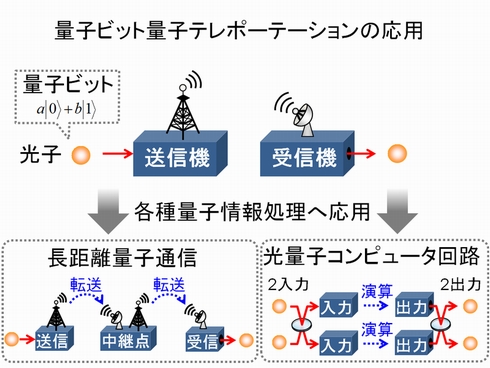
EETJ　どんなに距離が離れていても影響が及ぶ「量子もつれ」を利用した「量子テレポーテーション」として、2013年に「完全な量子テレポーテーション」を実証されましたが、どのようなものですか。

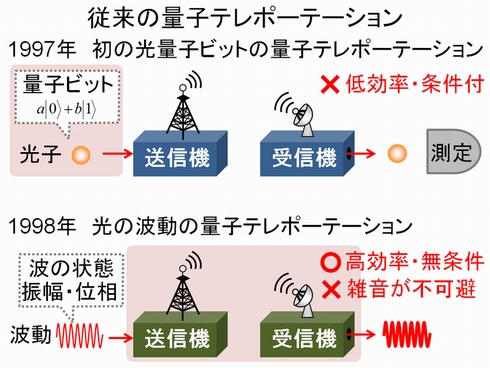
古澤氏　テレポーテーションの実験そのものは、十何年も前からいろいろな人たちがやっていまして、大きな流れとして2つのやり方がありました。量子というのは、波動性と粒子性という2つがあり、粒子性に着目したテレポーテーションと波動性に着目したテレポーテーションの2つでそれぞれ、十何年前から行われていました。

量子テレポーテーションの応用イメージ （クリックで拡大）

　そして2つの方法それぞれ欠点がありました。粒子の場合、効率が低いという欠点がありました。一方で、波動の場合は、成功のフィデリティー（忠実度）があまり上がらないという問題がありました。

従来の量子テレポーテーション （クリックで拡大）

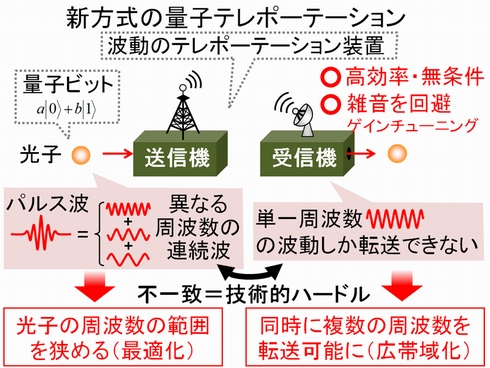
　われわれの「完全な量子テレポーテーション」というのは、粒子性/波動性テレポーテーションの両方の良いところをとって、効率が高くて、フィデリティーも高い量子テレポーテーションを世界で初めて成功させたということになります。

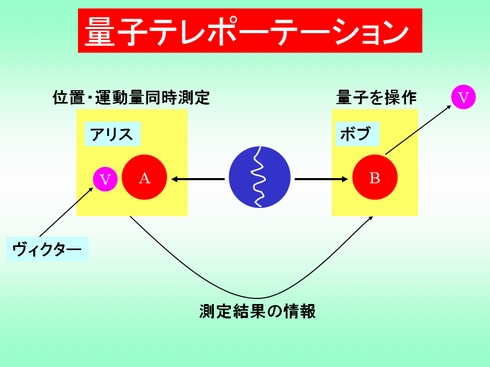古澤氏らが開発した新しい量子テレポーテーション （クリックで拡大）