人類は、“ダイエットに失敗する”ようにできている：世界を「数字」で回してみよう（15） ダイエット（7/9 ページ）

[江端智一，EE Times Japan]

（付録1）フーリエ変換とは何か

　「この世の中にある全ての時系列データは、sin関数だけで表現できる」と言われたら、多くの人は「嘘つけ！」と言うかもしれません。

　世の中に山ほど存在する無秩序なデータのグラフが、あのキレイなsin関数で表現できる訳がない ―― そう考えてしまうのは、自然なことです。

　でも、これ本当なんです（「サンプリング定理」で検索してみてください）。

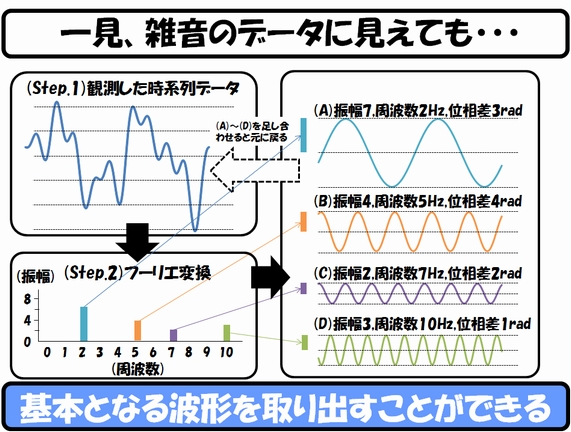
　まず、以下の図をご覧ください。

　観測した時系列データを、フーリエ変換（Fourier transform：FT）という方法で解析すると、その時系列データの中にどんな大きさのsin関数の波形が、いくつ含まれているのか、あっという間に分かってしまうのです。

　例えば、上図では観測データを変換すると、2Hz、5Hz、7Hz、10Hzの4つの波が、高さ7、4、2、3で存在していることが分かります。

　そして、バラバラにした波を、再びガッチャンコすると、元の時系列データに戻すこともできます。

---

　さて、今回は、ニュースの見出し（ニュースヘッドライン）の登場数の時系列データを使って、3つの周期性を見つけたのですが、これが実際どんな形の波をしているのかを見てみましょう。

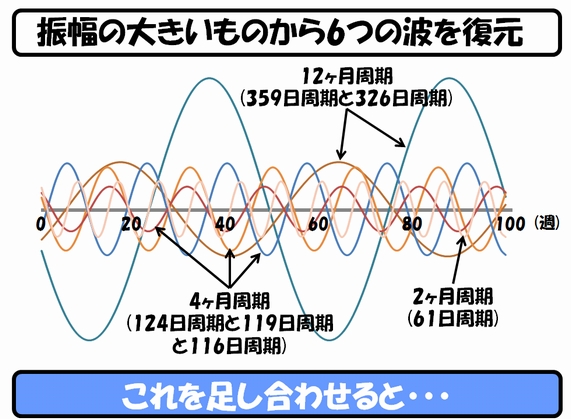
　最初に、振れ幅の大きかった12カ月周期（2つ）、4カ月周期（3つ）、2カ月周期（1つ）の波を、バラバラに書き出してみます。

　それぞれの波の高さが、その周期の振れ幅の大きさを示しています（位相補正済み）。全部キレイなsin関数になっていますよね。

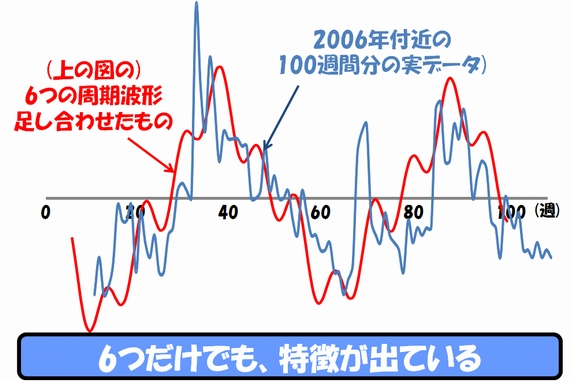
　では、この6つの波を足し合わせて、実際のデータと比較してみましょう。

　今回は、256の波形を取り出すことができるのですが、たった6つの波形だけでも、ざっくりした傾向をトレースできていることが分かると思います。

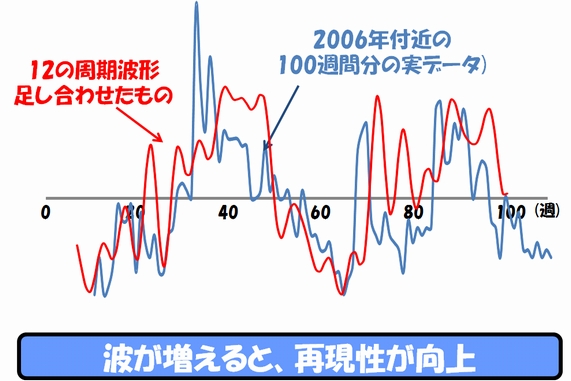
　この6つの波形に、さらに1.2〜1.5カ月周期の波を足し合わせてみたものが以下のグラフです。

　このように、フーリエ変換とは、一定時間で測定したデータであれば、そのデータの中に含まれる「繰り返し（周期性）」を簡単に見付けてくれる、大変便利な数学の道具です。

　昔、フーリエ変換をプログラムするのは結構骨だったのですが、今はエクセルで一瞬に計算できるようになっているみたいです。フーリエ変換の原理なんぞは知らなくても構わないので、数値データが手に入ったら、ぜひエクセルで遊んでみてください。今回の解析用のエクセルファイルは、こちらに置いてあります。