抹殺する人工知能 〜 生存競争と自然淘汰で、最適解にたどりつく：Over the AI ―― AIの向こう側に （7）（4/13 ページ）

[江端智一，EE Times Japan]

正規分布についてはどうするのか

　しかし、この段階では、選挙人の平均人数とその分散（標準偏差）が求まっているだけで、それが正規分布しているかどうかは分かりません。私は、この「合衆国選挙」の分散と感度だけに意識が向いており、正規分布に収束するかどうかについての検討を、すっかり忘れていました ―― というのはウソで、正規分布に収束するものと勝手に決めつけていました。

　シミュレーションの結果から、「どう見たって、これ、正規分布だろう？」と思えても、これが数学的に証明されなければ、正規分布として取り扱って出てきた結果（例えば、人工知能技術による推論結果など）には、常に不安がつきまとうことになります。

　逆に、「合衆国選挙」の選挙人の数が、正規分布に収束することが確定すれば、人工知能など登場させるまでもなく、一般的な統計解析手法で ―― 実際のところは、選挙の直前までに各州の精度の高い投票率（電話アンケートとか、街頭アンケートとか、インターネットのサイトとか）だけで ―― 超高精度の選挙予測が可能となるはずです^＊）。

＊）と言いつつも、投立する2人の立候補者の支持率が拮抗している時には、分散が極大となるので、相変わらず、当落判定が難しいことには変わりはないのですが。

　今回gauraさんは、リアプノフの中心極限定理を使って、「これ」を証明されました。

　これによって、第5回の「沈黙する人工知能 〜なぜAIは米大統領選の予測に使われなかったのか」の結論は、以下のように修正されることになります。

（修正前） 対象として理論上で捉えることが難しい
↓
（修正後） 対象として理論上で捉えることが可能である

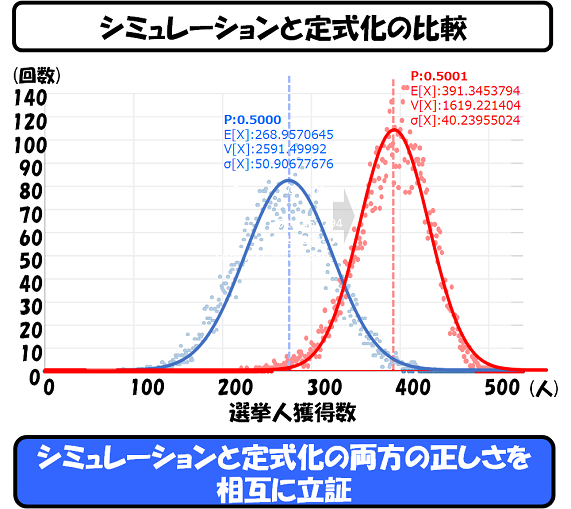
　以下に、シミュレーション結果と定式化による計算値の両方を図示したものを記載します。

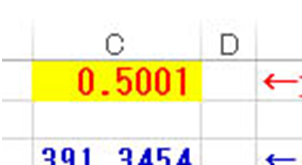
　こちらに、gauraさんからご提供いただいたエクセルシートに江端がグラフを追加したものを置いておきます。

　この黄色のセルの値（投票率）を変えるとすると、選挙の当選勝率が変わりますので、遊んでみてください（「200時間→0秒」に感激しているのは、私だけかもしれませんが）。

　しかし、このような定式化ができても、なお、正確な投票率を選挙前に知ることが難しいことと、やはり、p=0.5の時の感度（分散）が極大になることは、そのままですので、大統領選に対する当落予測が難しいことに変わりはないのです。

　しかし、考えうる最高精度の正確無比な投票数が、事前に判明するのであれば、人工知能技術なんか不要なのです。本当に、PCとエクセルとgauraさんの論理式があれば、十分なのです。

　あれ？　でも……。「考えうる最高精度の正確無比な投票数」って ―― それって、「投票を締め切った後の投票結果そのもの」ですよね。当落予測って、何のためにするんだったっけ？ ―― という感じで、私は今、ゲシュタルト崩壊の真っただ中にいます。