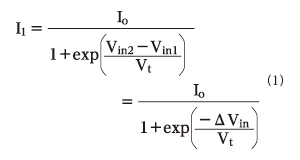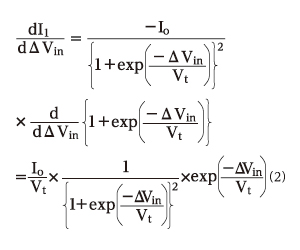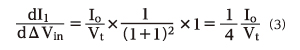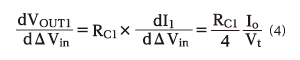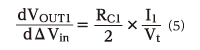第15回 差動対の利得を理解する:Analog ABC(アナログ技術基礎講座)(1/3 ページ)
今回は、差動対の利得に焦点を当てましょう。差動対は、例えばオペアンプなど、あらゆる増幅器の入力段に使われています。増幅器の重要な指標である利得について、理解を深めるのは大切なことです。
本連載の第13回以降、1対(2つ)のトランジスタで構成し、入力信号の差分に応じて動作する「差動対」の特徴や動作を紹介してきました(図1)。
前回(第14回)は、差動対の同相雑音除去と振幅の制限(リミッタ効果)の2つの特徴を使いながら説明しました。図1のコレクタ電流I1 とI2は、それぞれ入力電圧の差(Vin1−Vin2またはVin2−Vin1)で表現されているため、入力信号のうち同相成分は出力されないことが分かりました。これが同相雑音除去機能です。また、差動対では、Vin1とVin2がどのような値をとっても、I1またはI2はゼロからI0の範囲に収まり、振幅が制限されることを確認しました。
今回は、差動対の利得に焦点を当てましょう。差動対は、例えばオペアンプなど、あらゆる増幅器の入力段に使われています。増幅器の重要な指標である利得について、理解を深めるのは大切なことです。
利得とは、入力信号の変化に対する出力信号の変化具合を示したものです。従って、入力信号を横軸に、出力信号を縦軸にしたグラフでは、その傾斜が利得になります(図2)。傾斜は、出力信号を入力信号で微分することで求めます。
それでは実際に、利得を算出し、周波数特性を調べてみましょう。前回紹介したように、トランジスタQ1を流れるコレクタ電流I1は、以下のようになります(前回の(8)式)。
分母には、入力信号の差Vin2−Vin1があります。これが、差動対に対する入力信号ΔVinとなります。また、出力信号OUT1は、ドレイン電流I1と負荷抵抗RC1の積ですので、(1)式をΔVinで微分すれば、利得を求めることができます。
(1)式をΔVinで微分してみましょう。ここでは、合成関数の微分法を使いました。y=f(g(x))をxで微分するとき、y=f(u)、u=g(x)とすると、dy/dx =dy/du×du/dxになるというものです。(1)式では、f(u)が(u)−1、g(x)が1+exp(−x/Vt)に相当します。従って、(1)式の微分結果は以下の(2)式になります。
式(2)で最も利得が高くなるのはΔVin=0のときです。(2)式をさらにもう1回微分すると、ΔVin=0が変極点となり、利得が最大になることが分かりますが、ここでは省略しました。ΔVin=0のときの利得は以下のようになります。
VOUT1=RC1×I1の関係を使って、(3)式を変形します。
Δ Vin = 0のとき、I0=2 × I1ですので、最終的に利得は以下のように表せます。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- TIがSilicon Labsを75億ドルで買収する理由
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか

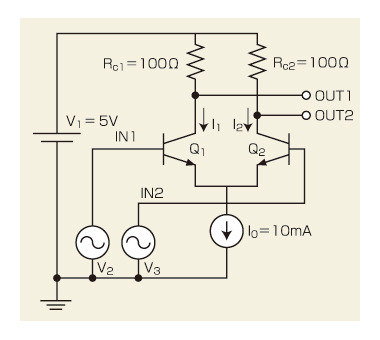 図1 差動対の回路例 今回は、差動対の利得を求めます。トランジスタQ1とQ2の動作のバランスによって、利得は変化します。
図1 差動対の回路例 今回は、差動対の利得を求めます。トランジスタQ1とQ2の動作のバランスによって、利得は変化します。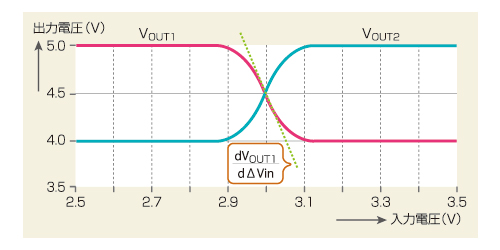 図2 出力信号の傾斜を求める 利得は、入力信号の変化に対する出力信号の変化具合を示したものです。入力信号を横軸に、出力信号を縦軸にしたグラフでは、その傾斜が利得になります。
図2 出力信号の傾斜を求める 利得は、入力信号の変化に対する出力信号の変化具合を示したものです。入力信号を横軸に、出力信号を縦軸にしたグラフでは、その傾斜が利得になります。