ダイエットを“過渡現象”で説明できるか：世界を「数字」で回してみよう（24） ダイエット（3/5 ページ）

[江端智一，EE Times Japan]

ダイエットを“過渡現象”で説明できないか

　ダイエットのデータを見ながら、ずーっと気になっていたことがありました。

　―― これって、「過渡現象^＊）」で、説明できないかな？

＊）システムが定常状態から別の定常状態に変化するときに、いずれの状態とも異なり時間的に状態が変化する非定常状態になる現象のこと

　人間の身体は、システムの一種ですから、以下の3つの説明変数があれば、ダイエット（減量）の動きを、一通り表現できると考えました。

1. エネルギーと（体重の要因となる）脂肪などの変換用の変数
2. エネルギーを脂肪などに変換せずに保管する変数
3. エネルギーの過激な流れを緩和する変数

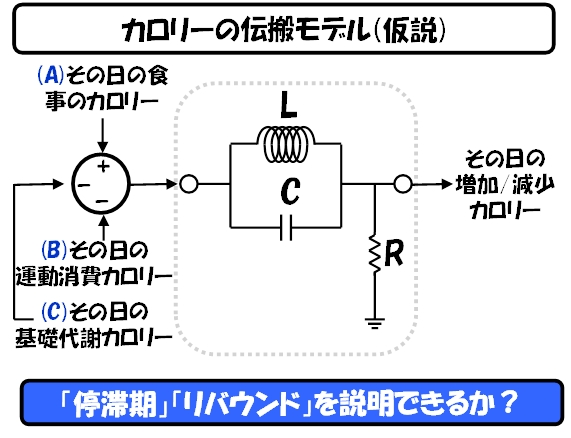
　これを電気回路のパラダイムを使って記述すると、以下のような、単純な回路図を使った伝搬モデルになりました。

　この回路図をぶっちゃけて説明すれば、以下のようになります。

　L（リアクタンス）とは、バイキングレストランで食べまくった影響が2日後に体重に反映される要素で、C（キャパシタンス）とは、夕食を抜いた日に、不足分のエネルギーを放出する要素を示します。

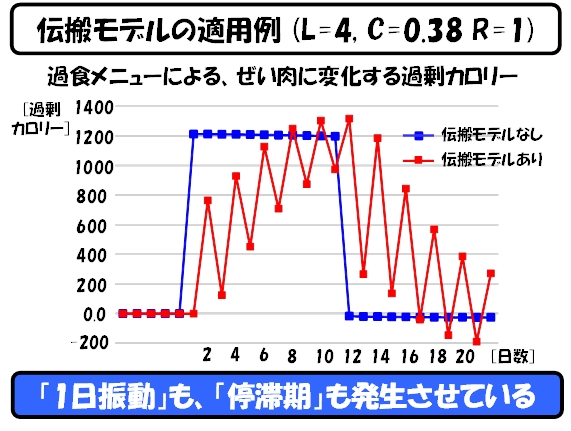
　この伝搬モデルのシミュレータの結果の1つを示します。

　これは、上記の「大食いシミュレーション」による過剰カロリーが、体重の増加分として変換される様子を示したものです。青色の線が、前回のシミュレータで使った値になります。一方、赤色の線は、伝搬モデルを組みこんだシミュレータの値になります。

　前述した、1日おきの体重の「バタバタ」を表現すると共に、時間遅れも発生させることで、「停滞期」も表現できているようにも思えました。

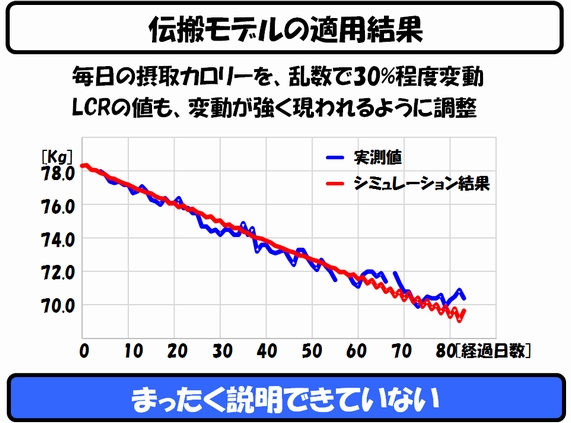
　この伝搬モデルのシミュレータを、前回作った「超シンプル体重シミュレータ」に組み込んで、実際に計算をした結果の1つを、以下に示します。

　結論から言うと、このモデルは、まったくダメダメでした。

　私の実測体重値の変化に対して、伝搬モデルの振幅幅は小さ過ぎますし、また、「停滞期」らしきものも出現していません。

　皆さんもご存じの通り、体重は、たった1日で0.5〜1kgも簡単に変動します。しかし、私のシミュレータでは、どんなに過食をしても、体重はたかだか160g程度しか変動できません。「7kcal＝1g」の式に縛られるからです。

　このような伝搬モデルを組み込んでも、私の作ったシミュレータでは、短期（数日から1週間）の体重予測をすることはできないことが判明しました。

　長々と説明した割には、しょぼい結果の報告となってしまい、私は、今、心の底から落ち込んでいます。