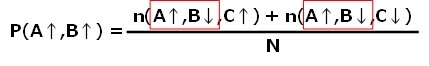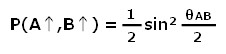量子もつれ 〜アインシュタインも「不気味」と言い放った怪現象：踊るバズワード 〜Behind the Buzzword（5）量子コンピュータ（5）（5/9 ページ）

[江端智一，EE Times Japan]

「ベルの不等式＝成立」の場合

　さて、ここから、再度、ベルさんにご登場いただきます。

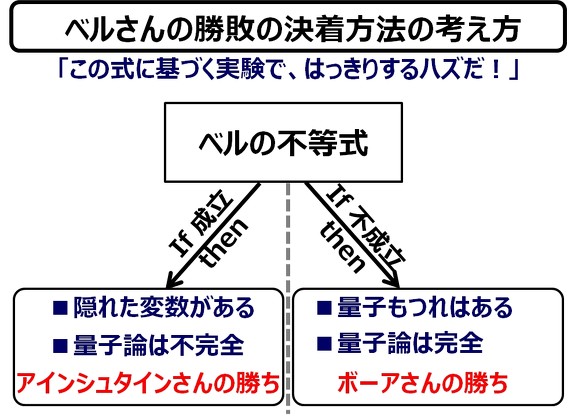
　ベルの不等式のすごいところは、「量子に局所性があるなら、不等式は破れない=アインシュタインさんの勝ち」、「量子の非局所性が成立するなら、不等式は破れる = ボーアさんの勝ち」という図式を、明快に示す点にあります。

　（ちなみにベルさんは、アイシュンタイン派「量子論は不完全」の方に属していたようです）

　ちょっと気を付けていただきたいのは、ベルさんは、この「ベルの不等式」を考えましたが、実証実験の方式（つまり、実験装置の作り方）までは提示していなかった、ということです。

　つまり「こういう実験ができれば、勝敗が付くはずだ」という可能性を、数式で示したものです。そして、現実の実証実験には、さらにここから8年の月日が必要でした（後述）。

　では、まずは「ベルの不等式」を使って、アインシュタインさんが正しいと仮定した場合の話から始めます。

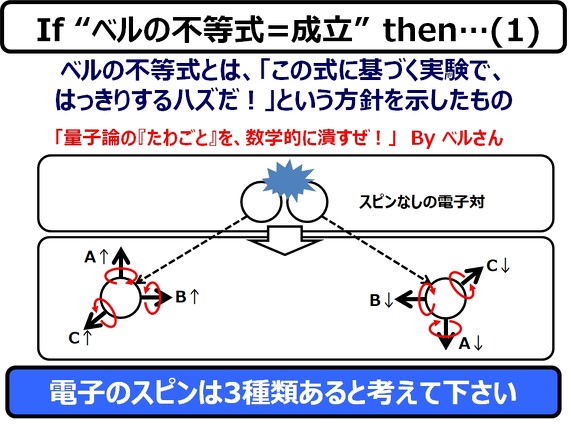
　電子のスピンとは、（詳しい話は省略しますが）基本的には、「概念」です。光速で移動している電子に回転があるとすれば、その回転速度は光速を超えてしまって、理論的に破綻してしまうからです。

　ですが、「スピンがある」として考えると、”電子に影響を与える”or”電子が作りだす”電場や磁場の影響をスッキリ説明できて、かつ量子論的にも矛盾が発生しないので、今回は、「スピン」を使って説明を強行します（というか、私（電子工学科出身）は、それ以外の方法では説明できません）。

　電子のスピンには（前述の”上向き”と”下向き”の）2つ、あるいは3つ、または4つとか、いろいろな考え方があります。今回の説明では3つのスピンを採用します。これはx,y,zとの3軸方向でのスピンと考えれば分かりやすいです。

　x軸方向に上向きのスピンを、”A↑”と、下向きのスピンを”A↓”と記載します。同様に、Y軸方向は、”B↑”、”B↓”、Z軸方向は”C↑”、”C↓”と記載することにして、その3つのスピンを（↑、↓、↑）などと記載することとします。この組み合わせは8（=2x2x2）通りになります。

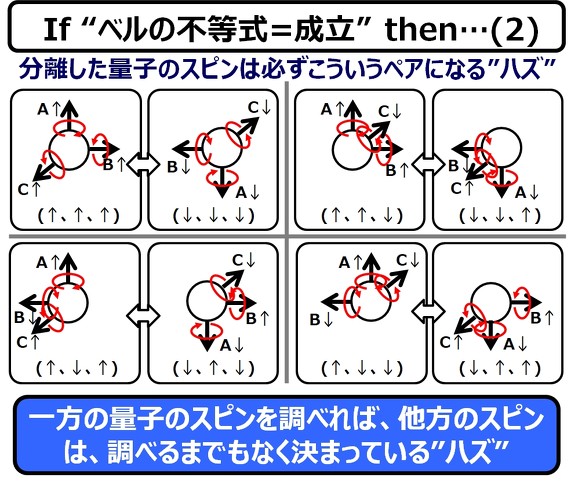
　先ほどお話した通り、分離させられた電子のスピンは、かならず逆方向になりますので（直感的にも分かりますよね）、例えば、一方の電子のスピンが（↑、↑、↑）ならば、もう一方の電子のスピンは、測定するまでもなく（↓、↓、↓）となっているハズです。この対となるペアを記載したのが以下の図です。

　ここで、電子のスピンを測定する測定器の一つは、地球上にある江端家にあり、もう一方の測定器は、江端の出張先の木星大気圏探査艇の中にある、と仮定します（あくまで、思考実験です）。

　木星と地球の中間地点くらいで、電子対から分離した電子を、膨大な数、ランダムな方向にぶっぱなし続けるとします（電子の量子状態の時間（コヒーレント時間）は無視します）。

　その（気の遠くなるほどの小さい確率で到着した）一部の電子を、地球と木星の両方で、とにかくカウントし続けるとします。

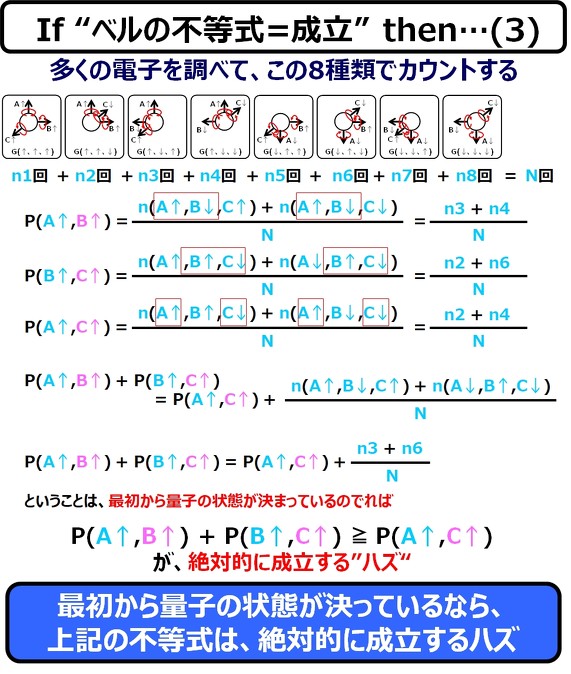
　地球上でX軸を観測して上向き（↑）となり、木星軌道上でY軸を観測して上向き（↑）となるような確率Pは、

と、表せます。ならば、P（B↑、C↑）も、P（A↑、C↑）も同様に表せるハズです。

［Tさんツッコミ！］この式の意味が分かりにくい気がします。PはP（地球、木星）の測定結果になる確率で、nはn（地球X、地球Y、地球Z）の測定結果で、nはその場合の数、Nは全部の場合の数（8ケース）ですね。地球と木星で色分けするとよいかもしれません。

（というアドバイスを頂きましたので、以下、地球は水色で、木星はピンクで示します）

　ここでは、スピンの方向がX,Y,Z軸と記載したので、あたかもスピンが直交しているように見えるかもしれませんが、このX,Y,Zは、全く同じ軸（角度0°）でなければ、どの方向に向いていたって構わないものとします。

　もし、X,Y,Zがキレイに直交していなければ、n1〜n8回の個数は、平均的にはならず、かなり偏ったものになるかもしれません（例えば、n3=0, n6=0というような極端なケース）が、それでも、この不等式が破れることはありません^＊）。

＊）試しに、n1〜n8に好きな数（0以上の整数）を入れて計算してみて下さい。

　ベルさんのすごいところは、「もし確率に基づく量子論が成立するなら、この不等式を破れる」ということを示したということです^＊）。

＊）私には、ベルさんが「できるものなら、この私の不等式を破れる実証実験結果を見せてみな！」と、ボーア派を挑発しているように見えました。

　では、次に「ベルの不等式」を使って、ボーアさんが正しいと仮定した場合の話から始めます。

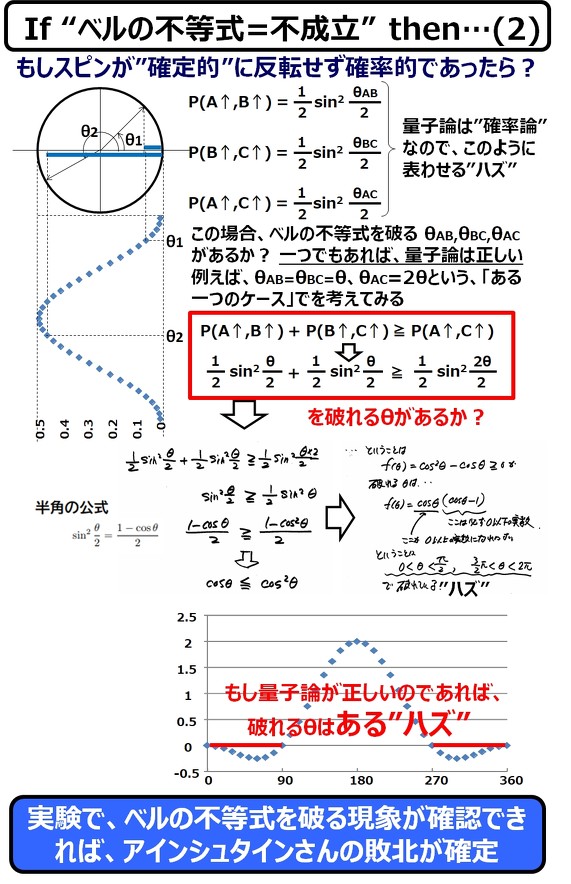
　こちらでは整数は登場しません。徹頭徹尾、確率（％）を使います。

　この式の意味は意外に簡単です。

　これは、片方の量子の回転が反転（180°）する確率が1/2になることを示す式である点では、「アインシュタインさんが正しいと仮定した場合」と同じです。

　しかし、この式では、確実な反転（180°）だけではなく、中途半端な反転である、179°も181°の存在はもちろん、123°だって、32°だって、下手すれば、0°の可能性すら、「確率は小さくなるけど、それでも存在するハズ」を示す式になっています ―― まさに「確率に基づく量子論」を体現している式と言えます。

　故に「量子論が正しい」を証明するには、ベルの不等式の反例が一つ見つかれば十分なのです。

　で、実際に、ある特定の条件下（図中の例では、θ_AB=θ_BC=θ、θ_AC=2θとして式を組み立てています）では、ベルの不等式が破れる値が、バッチリ存在するのです。

　だからベルさん（アインシュタイン派）の、ボーア派への挑発（？）とは「実証実験で、この不等式の反例を1つでもいいから、見つけてみやがれ」ということになるのです。