量子もつれ 〜アインシュタインも「不気味」と言い放った怪現象：踊るバズワード 〜Behind the Buzzword（5）量子コンピュータ（5）（7/9 ページ）

[江端智一，EE Times Japan]

2量子ビット／ゲート

　さて、ここから今回の本論「2量子ビット/ゲート」についてお話したいと思います。

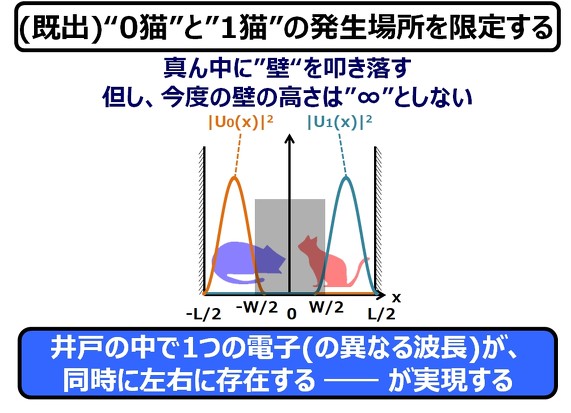
　以前、1量子ビットゲートの時に登場させた、1量子ドットビットを実現する、量子井戸の説明をしました（関連記事：「量子コンピュータよ、もっと私に“ワクワク”を」

　基底状態の電子（通称”0猫”）と、第1励起状態の電子（通称”1猫”）が、半導体の井戸の中の左右に、確率50％で存在する1量子ビットです。

　で、この量子井戸に対して、ラビ振動を有する電磁波の照射を行うことで、1量子ビットを制御することができることは、「量子ビットを初期化する 〜さあ、0猫と1猫を動かそう」で説明しました。

　2量子ビット/ゲートについても、量子井戸で説明します（というか、江端が説明可能なデバイスって、この量子井戸ぐらいしかないので）。

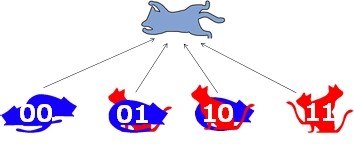
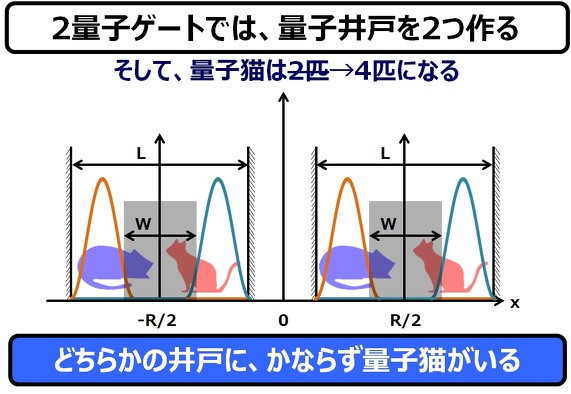
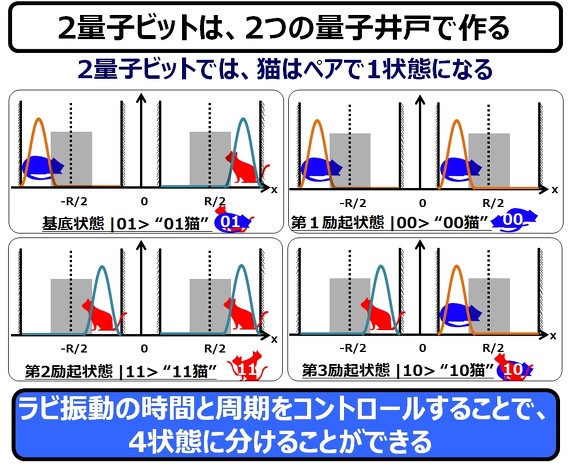
　2量子ビット/ゲートでは、「井戸を2つ掘って、量子ネコを2匹（“0猫”と”1猫”）から、4匹（“00猫”、”01猫”、”10猫”、”11猫”）に、増量させます。

　2量子ビットのデバイスに関する資料は、（1量子ビットに比べると）ものすごく少なくて、本当に困っていたのですが、「14日で作る量子コンピュータ」（遠藤理平／2020年）だけは、2量子井戸の実現方法が具体的に記載されていました。

　私、数式を数式のまま理解することは、からっきしダメなのです。しかし、それがプログラムで記述されて、実際の数値に落し込めれば理解ができるという現場系（ガテン系）のエンジニアです。

　ですので、この本（以下”14日本”と称呼させて頂きます）を読む度に、『私のために書いてくれたの？』と目がウルウルとしてきます。

　まあ、それはさておき。

　それでは、4状態の量子猫が、井戸に鎮座している状態を図示してみます。

　こんな感じで、2量子ビット（ここでは、2量子ドットビット）が実現されることになります。

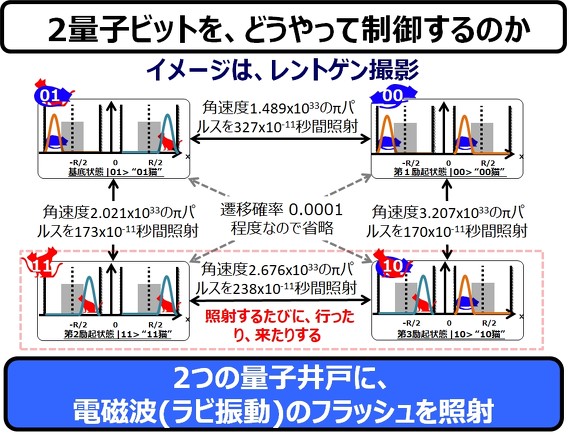
　で、この2量子ビットをどのようにコントロールするかというと、やはりこちらも、1量子ビットと同様に、電磁波のπパルスの照射時間で制御します。ただ、周波数（角速度）は超高速で、その照射時間も超短時間であり、そのコントロールの難しさは、1量子ビットよりさらに困難なものとなっています。

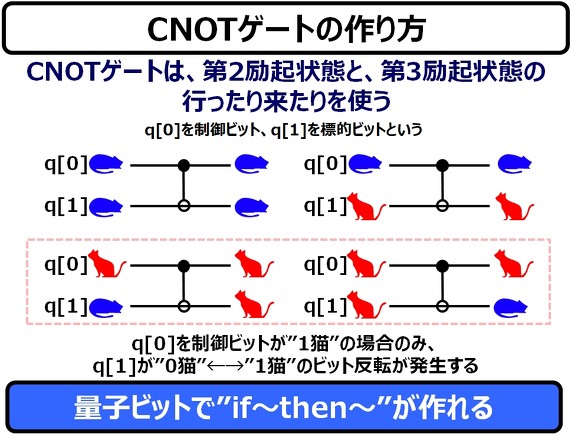
［Tさんツッコミ！］第2と第3励起状態に共鳴したπパルスを照射することで、CNOTが実現されるということですね。

　同じ内容のラビ振動の照射を行うことで、2状態の電子猫の状態を行ったり来たりさせることができます。

　さて、今回は2量子ビットを使う2量子ゲートの中でも、もっとも有名なCNOT（制御NOTゲート）を紹介します。これは、前半で簡単に説明した「量子もつれ」を作り出すのに必須の2量子ゲートであり、また、前回のコラムでTさんから、以下のようなツッこみを頂いていたためでもあります。

［Tさんツッコミ！］CNOTゲートなどの2量子ビットゲートは、IF-THENの量子ビット版に対応していると考えることもできませんか？　制御ビットが0か1かで、標的ビットにNOTをかけるかどうかが切り替わります。

　なるほど ―― 制御ビットq[0]に”1猫”をセットして、「はい、息を止めて〜、バシャ！」という、レントゲン撮影のように、ラビ振動の電磁波照射をすれば、標的ビットq[1]の猫が入れ替わります。しかし、q[0]に”0猫”をセットすれば、q[1]の猫は変化しません ―― これは、量子ゲートで、”if〜then〜”が実現されていることを示しています。

　このCNOTゲートの存在によって「量子コンピュータ」は、確かに「コンピュータ」であると言えます。”if〜then〜”がない計算機は、単一目的の演算器に過ぎませんから。

「量子もつれ」の作り方

　では、今回のメインであるところの、量子コンピュータにおける「量子もつれ」の作り方のお話に入ります。

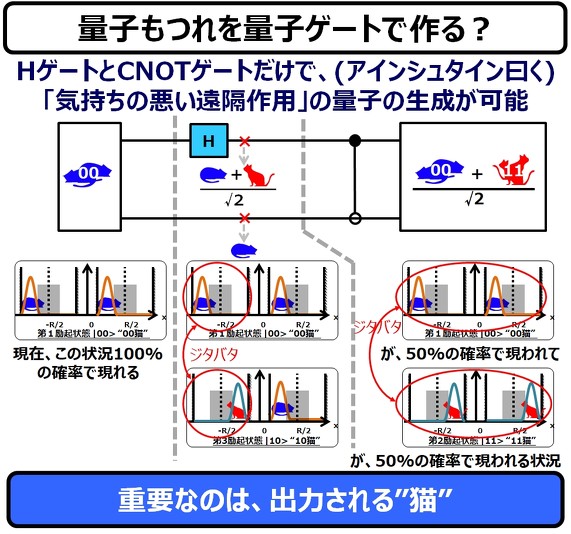
　「量子もつれ」は、前回説明したHゲート（アダマールゲート）と、CNOTゲートを以下のように組み合わせることで実現されます。

　順を追って説明します。最初の状態では、第1励起状態（×基底状態）の”00猫”がいるだけです。しかし、この”00猫”を、アダマールゲートに放り込むことによって、”00猫”と”10猫”が、共存する状態になっています。

　もし、アダマールゲート通過後の、この井戸を観測できたとしたら、右側の井戸の猫（1ビット目の猫）だけが、ジタバタ動いている（あるいは両方が、うっすら透過して）見えるハズです。

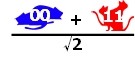
　そして、最後にCNOTゲートを通過することで、 “00猫”と”11猫”が確率50%で出てくる電子猫が出てきます ―― が、

　ぶっちゃけ、私にとっては、そんなことはどーでもいいのです。

　問題は、なぜこのようにして生成された2量子ビットが「特別」であるか、すなわち「2つの量子ビットのうち、どちらの状態を観測すれば、その観測結果に応じて、もう片方の量子ビットが確定する」という不思議な（気持ちの悪い）量子ビットになっているか、ということなのです。

　いろいろ調べたのですが、私の頭でなんとか理解できた内容は、”14日本”のP.209ページに記載されていた、「量子もつれ（量子エンタングルメント）の生成方法」です。以下に、私なりの理解を記載させて頂きます。

（ここから）

　仮説：2つの量子が「もつれていない」、つまり、単なる「重ね合わせ」だけで存在しているなら、

は、「重ね合わせ」の式でだけで表現できるはずである。

　すなわち、

X猫 = x₀ 0猫 + x₁ 1猫
Y猫 = y₀ 0猫 + y₁ 1猫

となる。

　これまでのように「重ね合わせ」の式のまま展開すると

XY猫 = x₀ y₀ 00猫 + x₀ y₁ 01猫＋x₁ y₀ 10猫＋x₁ y₁ 11猫

となるはずである。

　検証：今, XY猫 = 1/√2 （00猫 + 11猫）であるから、これを当てはめると、x₀ y₀ = x₁ y₁ = 1/√2 , x₀ y₁ = x₁ y₀ =0になる。しかし、そのようなx₀、x₁、y₀、y₁は、存在しない（実際に調べれば明らか）。

　結論：これまでの連載で散々使ってきた量子計算のかけ算（テンソル積）を、どんなに複雑に使い倒したとしても、

は、絶対に作り出せないということである。

　これこそが、一方の量子の状態に、他方の量子の状態が、ズルズルとひっぱられてしまうことの証明、すなわち「量子がもつれている」ということである。

［Tさんツッコミ！］このため、よく量子もつれ状態は、「因数分解できない状態のこと」と説明されます。