株価データベースを「Docker」で作ってみる：「お金に愛されないエンジニア」のための新行動論（4）（3/12 ページ）

[江端智一，EE Times Japan]

「工学」と名が付けば、こっちのもんだ

　“工学”とさえ名前が付けば、こっちのもんだ ―― とばかりに、私は金融工学について調べ始めました。

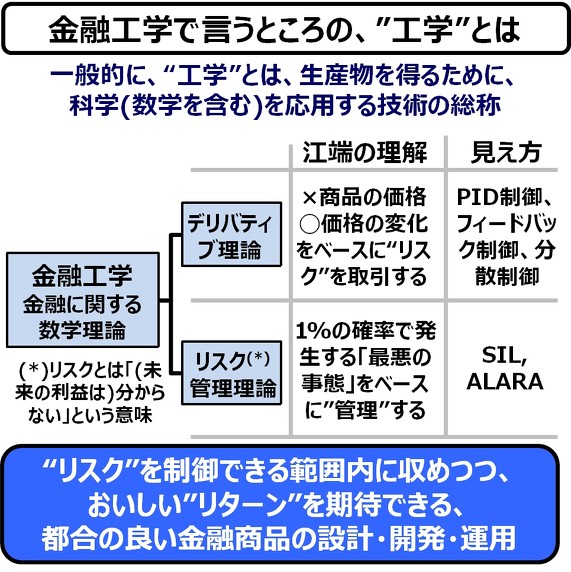
　金融工学とは数学理論です。その理論は、大きく2つに分類されます。（1）デリバティブ理論と（2）リスク管理理論です。

　まず、（1）デリバティブ理論ですが、これを簡単に言うと、「商品の価値そのものは、どーでも良くて、その価値の変化から生じる価値（リスク）を商品とする」というものです。

　このデリバティブでよく使われるネタが、「熱々ラーメン屋」と「冷やし中華屋」のデリバティブです。熱々ラーメン屋は、気温が上がるとお客が来なくなり、冷やし中華屋は気温が下がるとお客が来なくなます。

　気温30℃をしきい値として、30℃を下回る気温に比例して「熱々ラーメン屋」→「冷やし中華屋」に売り上げを渡し、逆に30℃を上回る気温に比例して「冷やし中華屋」→「熱々ラーメン屋」に売り上げを渡す、というものです。このデリバティブはスワップ取引といわれるもので、このケースでは、気温の”変化”というリスクが、金（債券）になる訳です。

　これを工学的な視点で見れば、PID制御の中のP: Proportional（比例）制御であり、「熱々ラーメン屋」と「冷やし中華屋」の2つサブシステムから成るシステムによる、分散・フィードバック制御とも言えます。

　問題は、ここに「熱々ラーメン屋」でも「冷やし中華屋」でもない、全く関係のない第三者が関わってくる、ということなのです。その第三者にとっては、ラーメンや冷やし中華がどうなろうと知ったことではありません。両方の店が潰れようとも、自分さえもうかれば、それで良いからです。その第三者からすれば、極端な猛暑も、記録的な冷夏も、大もうけの（あるいは大損害の）チャンスとなるのです。

　次に、（2）のリスク管理理論ですが、ここで言う”リスク”は、私たちが普段扱っている”リスク”とはちょっと意味が違います。ここでのリスクとは”危険である”ということではなく、”予測できない”ということです。

　そういう意味では、SILとか、ALARAのような工学的な安全性とも少し違います。SILやALARAは、稼働時間に対する故障の発生率で測るものです。飛行機をSILで語るのであれば、墜落するような故障の平均時間が、人間の一生（ざっくり100年間）よりも十分長い時間になるならば、その飛行機は「安全である」と言い張ってもいい、ということです（ちなみに、永久に安全であるような乗り物なんか、この世には存在しません）。

　一方、金融商品は、経年劣化する部品もなければ、ヒューマンエラーによる事故も考える必要はありません。金融商品で考えることは、（1）値上がりするか、（2）値下がりするか、（3）（会社が倒産して）紙くずになるか、の3つのパターンしかありません。今は、（3）の絶望的なリスクをいったん忘れるとして、（1）（2）についてのリスクとは、値下がり、値上がりが『どの範囲で収まるか』が分からん、ということなのです。

　金融工学によって作られた金融商品は、『リスクをどの範囲で収めるか』を、あらかじめ組み込んで設計・開発される、という点において、他の債券（株、社債、国債など）とは異なるのです。

　こういう金融商品は、買い手にとっても安心があります。そもそも金融商品というのは、なんであれ「わけあり商品」です。常に損害の可能性があり、最悪、紙くずになる恐れすらあるからです。比して、金融工学技術によって作られた商品は、その「わけ」が、パッケージに印刷されている点において異なるのです。

　その「わけ」の大本（おおもと）となっているものが、標準偏差です。

「偏差値」からおおよその未来が分かる

「未来を占う人工知能 〜人類が生み出した至宝の測定ツール」

　私は、標準偏差から導かれる偏差値は「人類が生み出した至宝の測定ツール^＊）」と言い切っています。そして、現在の学校教育を『偏差値教育』なる名前をつけて批判する大人たちに対して、

―― 何をバカなことを言っていやがる

と、今でも言い続けています。

　『偏差値教育』を批判する人間に対して、私は、「縁故主義」「血縁主義」「カルト主義」「人格主義」なるものを挙げた上で、「偏差値の替わりとなるものを提案した上で、批判してみろ」と、煽り続けています（関連記事「未来を占う人工知能 〜人類が生み出した至宝の測定ツール」）。

　それはさておき。

　一般的に株価は、その時点における将来の予想が反映されています。例えば「新規事業が快調だから売り上げが伸びそうだ」とか、「ウクライナ戦争で原油価格が高騰するので減収しそうだ」などという予測に基づいて、投資家は株の売買を行うわけです ―― もし、そのような事前の公開情報だけで株価が、確定的に決定しているのであれば、株価の変動による利益や損益も発生しないはずです（理屈の上では）。

　それでも、なぜ株価が変動するかというと、現時点では不明な情報によって、株価に対する判断が投資家によって異なるからです。そして、その「不明な情報」が、株価を上げる材料になるのか、下げる材料になるのかは、分かりません。

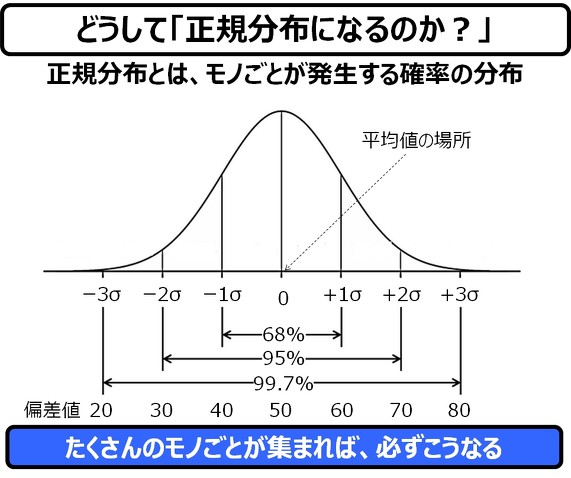
　このような、確実性のない株価の変動は、「酔っ払いが千鳥足で歩いている」のと同じようなものであると考え、このようなランダムな動きを、「ランダムウォーク」と言います。そんでもって、この「ランダムウォーク」は、ランダムであるのにもかかわらず、ある法則に縛られます。それが正規分布です。

これが「ランダムウォーク」だ

　下記の図は、Excelで乱数関数を使ってランダムウォークをさせてみた結果です。ファイルはこちらからダウンロードできます。

　簡単に言えば、（1）最初の場所（0メートル）を中心に、そこから遠ざかっていくウォーカーの数は少なくなっていく、（2）時間の経過とともに、遠ざかっていく距離は長くなっていく、ことが分かると思います。そして、ある距離に到着する確率は、必ず、以下のような正規分布になるのです ―― 必ずです。

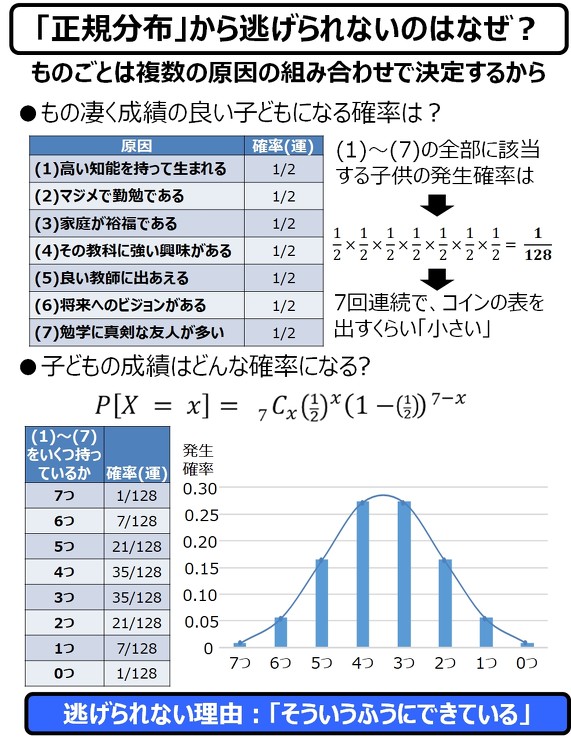
　以下の図は既出ですが、私たちが正規分布からから逃げられない好例と思いますので、再掲いたします。

　この正規分布の中心を平均値と言い、広がり具合（幅）を標準偏差といいます。この平均値と標準偏差は、現実の株価の動きを観測し続けることで、求めることができます。または、設計段階の金融商品であれば、前述した「1000億本ノック」のモンテカルロシミュレーションで求めることもできます。

　そんでもって、この平均と標準偏差の2つさえ分かれば、「標準正規分布表」を用いて、この現象の、おおよその未来が、”今”、分かってしまうのです ―― これこそが偏差値が導くミラクル（奇跡）なのです。