第6回 エミッタ接地回路の定数を決める:Analog ABC(アナログ技術基礎講座)(3/3 ページ)
「鳳-テブナンの定理」を活用
以上の情報から、抵抗R1とR2を決めるための回路が図4です。図4(a)はR1とR2、トランジスタのベース端子の部分を抜き出して書いてあります。電子回路の授業で真っ先に学習する「鳳-テブナンの定理」を使うと図4(b)のように変換できます……と書いてしまうとそれまでなのですが、筆者は、この定理を教わった学生のときはいったい何に使うのか分かりませんでした。
詳しく説明しましょう。図4(a)のVbは、Vccを抵抗で分圧した値なので、Vb=Vcc×R2/(R1+R2)と計算できます。図4(b)に示したVbを、図4(a)のVbと同じ値にするには、V2をV2=Vcc×R2/(R1+R2)とすればよいことが分かります。
しかし、仮にR1とR2の合成抵抗値であるR3が無ければ、負荷電流(ここではベース電流)による電圧降下が発生しません。そこで図4(a)の「Vb」と記載した端子の外から回路の中をのぞき、Vb(出力)端子とグラウンドとの間の抵抗成分(出力インピーダンス)を計算します。この抵抗成分に相当するのが図4(b)のR3で、図4(b)でも出力インピーダンスが図4(a)と同じになるようにR3の値を設定します。
図4(a)の出力インピーダンスを考えるとき、Vccを発生させる電圧源は短絡とみなし、抵抗は0Ωです*4)。従って、R1と電圧源の抵抗値0Ωの和と、R2の並列抵抗値「R1×R2/(R1+R2)」が図4(a)の出力インピーダンスとなります。図4(b)でR3=R1×R2/(R1+R2)とし、V2=Vcc×R2/(R1+R2)とすれば図4(a)と図4(b)はまったく同じ回路になります。これは、鳳-テブナンの定理そのものです。筆者がこの定理を実際の回路でどのように使うかを知ったのは、アナログ回路を設計する仕事に就いて数年たってからのことした。
R1とR2の値は次のように計算します。図4(b)で、R3を先ほど計算した500Ω、R1とR2でV1を分圧した電圧V2が、860mV+130mV=990mVとすれば良いのです。従って、R1とR2は次の2つの式から、R1=2.525kΩ、R2=623Ωが得られます。
温度特性に難あり
以上の説明で決めた定数を使ったエミッタ接地増幅回路を図5に示しました。前段または後段の回路に入力/出力のバイアス電圧が影響されないように、入力部分と出力部分に1μFのコンデンサ(C1とC2)を付けました。入力信号を印加したときの過渡解析した結果が図5(b)です。目標通りに、10mVppの入力電圧幅に対して、1Vpp幅の出力電圧が出力され、ほぼ期待通りの結果が得られました。
せっかく増幅回路を設計したので、温度特性がどのようになるのかをシミュレーションで確認してみました。周囲温度を−40℃、27℃、125℃と変えて計算したところ、125℃の周囲温度では出力電圧の下側が歪んでしまいました。図5(a)に示した増幅回路には、温度特性が悪いという欠点があることが分かります。125℃の高温環境で使うことは無いのではと、思うかもしれませんが、自動車のエンジン・コントロール・ユニットならば十分にあり得る温度です。そこで次回は、温度変化への対策を紹介しましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか

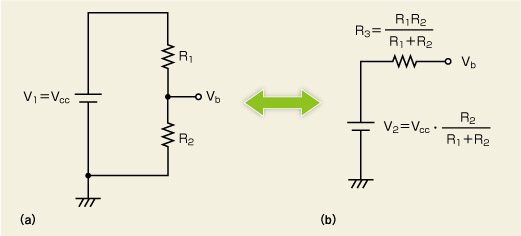 図4 R1とR2を決めるための回路変換 (a)と(b)はまったく同じ回路です。R1とR2の値を決めるために、電子回路の基本定理である「鳳- テブナンの定理」を使います。
図4 R1とR2を決めるための回路変換 (a)と(b)はまったく同じ回路です。R1とR2の値を決めるために、電子回路の基本定理である「鳳- テブナンの定理」を使います。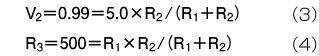
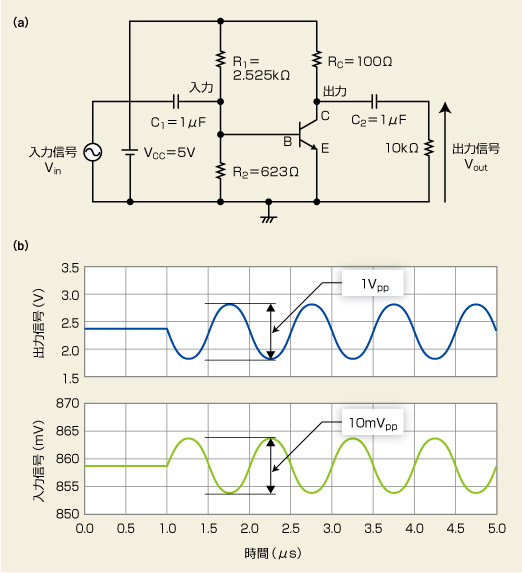 図5 目標通りに回路設計が完了 (a)は今回設計した増幅回路の全体です。(b)では、「10mVppの入力電圧を、1Vppに増幅して出力する」という目標通りに回路が設計できたことを示しました。
図5 目標通りに回路設計が完了 (a)は今回設計した増幅回路の全体です。(b)では、「10mVppの入力電圧を、1Vppに増幅して出力する」という目標通りに回路が設計できたことを示しました。