未来を占う人工知能 〜人類が生み出した至宝の測定ツール：Over the AI ―― AIの向こう側に（19）（6/11 ページ）

[江端智一，EE Times Japan]

野球でもワインでも統計技術が使われている

　では、ここからは統計解析技術についての2つ目のお話として、「回帰分析」という手法についてお話します。

　専門家のカンがほとんどアテにならず、数字を使った解析の方が、よっぽど役に立つということを、野球のゲーム解析で明らかにしたのが、「マネーボール」^＊）でした。

＊）実在する、メジャーリーグの貧乏球団が、統計解析手法（セイバーメトリクス）と呼ばれる独自の手法を用いて、プレーオフ常連の強豪チームを作り上げていく様子を描いた本。2003年に米国で発売され、ベストセラーになった。2011年にはブラッド・ピット主演で映画化されている。

　「その数字が戦略を決める」などでは、冒頭に、20年後のワインの品質を予測する式を、産地の気象条件（温度、雨量等）をパラメータとした線形の方程式にして、算出する方法を紹介しています。

　この方法は当初、専門家たちに酷評され、嘲笑されていました。ですが、その方程式による予測があまりに正確だったため、逆に専門家たちは面目をつぶされてしまい、今や20年後のワインの品質を評価する方法として、専門家自身がその方程式を使うようになっています。

　上記の野球もワインも、ある条件と結果の相関関係を見つける統計処理を行ったものです。この相関関係を見つける方法として、単純な線形方程式を用いるものを「回帰分析」と言います。（確かに、データが「回って」この方程式に「帰って」くるというイメージなので、優れたネーミングと言えます）。

「回帰分析」をおさらいしよう

　難しい話は抜きにして、回帰分析をざっくりと説明しましょう。

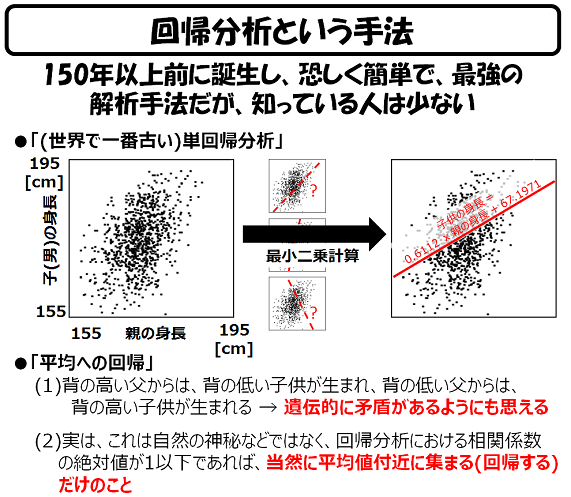
　上記は、イギリスの科学者フランシス・ゴールトン卿が集めた親の身長と子ども（男児）の身長のデータです。ゴールトン卿はこれらのデータから、その関係を表す1本の線（y=Ax+B）を導くことで、子どもの身長を予測しようと考えました。

　それには、最小二乗法という計算が必要でした。その1本の線（y=Ax+B）と各データの距離の差を一番小さくする線を求めるものです。コンピュータのない時代では、手で計算しなければならなかったので、かなり面倒だったと思いますが、今なら「エクセル」を使えば一瞬にしてA,Bの値の他、寄与率やら誤差の標準偏差やらもまとめて、計算結果を出せます。

　なお、ゴールトン卿は「平均への回帰」という現象を発見したことでも有名です。私はこれの意味が良く分からなかったのですが、なんのことはない、上記の図のグラフの傾きは0.612ですので、親の身長のバラツキよりも、子の身長のバラツキは0.6倍ほど控え目になる、ということです。

　つまり、子の身長のバラツキは、親の身長のバラツキよりも小さくなり、平均値へ集まりやすくなる、ということです。

　回帰分析も、AI技術以前の古典的手法ですが、今でもAmazonの「One to Oneマーケティング（個人ごとに宣伝広告の内容を変える）」、出会い系のマッチングサイト、あるいは、カード会社が解約しそうなユーザーを事前に発見して、それをつなぎとめる手法として使われています（これまで、どんなユーザーが解約してきたかを、記録しておき、回帰分析しておく）。

　私が行った回帰分析としては、以前、「部分痩せは可能なのか？ （後編）」で、

『女性は太る時には、ウエストから大きくなり、足、顔、そして最後にバストが大きくなります』
『しかし、ダイエットをすると胸から小さくなっていき、最後にウエストが細くなるのです』

という担当Mさんの主張に対して、私は、この回帰分析を使って、この現象が「錯覚と思い込み」であることを数理的に論証しました。

　この時はたまたま、アイドル、芸能人、一般人の女性の体格データが入手できたから、解析することができたのですが、多くの場合、大量のデータの入手は困難です。

　以前、私は「どこにも存在しないビッグデータ」で書きましたが、“ビッグデータ”と気楽に言われるほど、大量のデータというのは存在せず、入手できないものなのです。