EE Times Japan >
連載記事 >
中堅研究員はAIの向こう側に“知能”の夢を見るか:Over the AI ――AIの向こう側に(1)(7/8 ページ)
» 2016年07月27日 11時30分 公開
[江端智一,EE Times Japan]
ルールベース推論の問題点
ところが、このルールベース推論には問題があります。
まず、上記の10個のルールのいずれにもひっかからない場合、コンピュータは推論結果を導くことができません。
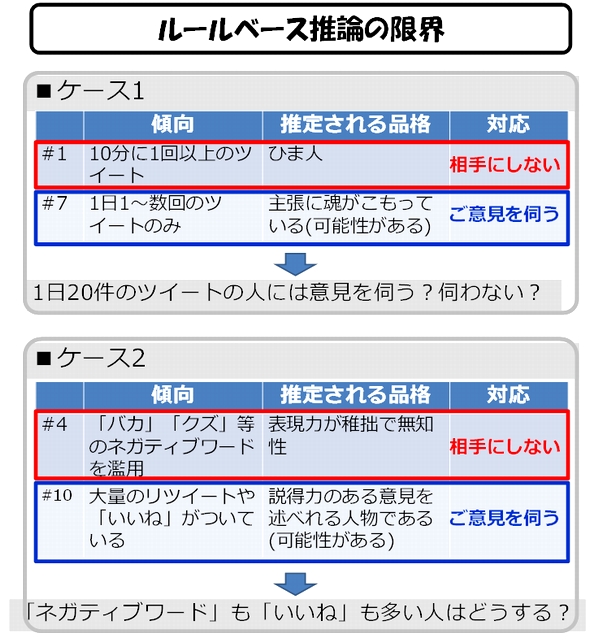
さらに、厄介なことは、2つのルールが相反する結果となる場合です。
例えば、以下のようなケースです。
しかし、ファジィ推論のすごいところは、たったこの10個のルールだけをつかって、どんな状況にあっても、きちんと推論結果を出してくる、という点にあります。
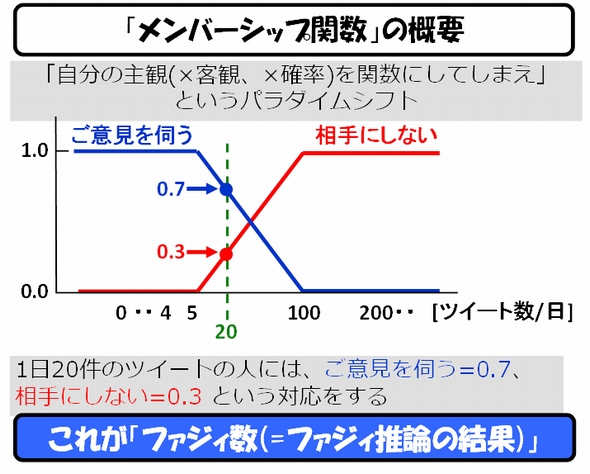
これが「メンバーシップ関数」と、「ファジィ数」という、コロンブスの卵の発想にあります。
このメンバーシップ関数の入力は、0以上無限大までの整数が入力できますので、ルールを追加する必要はありません。また、ファジィ推論の最終結果はファジィ数として出力されます。
ふざけてんのか?と思われる方もいるかもしれませんが、これは全く真面目な話で、ファジィ推論の結果は、常にファジィ数(例:ご意見を伺う=0.7,相手にしない=0.3)という形で出力されます。
もっとも、ファジィ数のままでは、使いものになりませんので、一般的には、ファジィ数を構成する値の中で一番大きいものを選ぶのが普通です(このケースでは、「ご意見を伺う」となる)。
複数のメンバーシップ関数と、ファジィルールを組み合わせる方法としては、多くのケースで、min-max簡略ファジィ推論法というものが使われています。プログラミングはちょっと面倒ですが、理屈は単純ですので、興味のある方は、こちらを御参照ください。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
記事ランキング
- ローム、TSMCのライセンス取得し650V GaNパワー半導体を自社生産へ
- 定年間際のエンジニアが博士課程進学を選んだ「本当の理由」
- Intelとソフトバンク子会社が次世代メモリ開発へ 29年度に実用化
- TIがSilicon Labsを75億ドルで買収する理由
- AIは「バブル」ではない――桁違いの計算量が半導体に地殻変動を起こす
- ソシオネクスト増収減益、中国向け車載新規品は順調に増加
- AI時代のニーズ捉え開発加速、キオクシア次期社長の展望
- SAIMEMORYの新構造メモリ 低消費電力に焦点
- 三菱電機の半導体は光デバイス好調 3Q受注高49%増
- TSMCは2nmで主導権維持、SamsungとIntelに勝機はあるか
Special SitePR
あなたにおすすめの記事PR