万年ダイエッターにささげる、“停滞期の正体”：世界を「数字」で回してみよう（22） ダイエット（6/10 ページ）

[江端智一，EE Times Japan]

無限に太り続けないのは、なぜなのか？

　ところで皆さんは、ダイエットをしていない時に、無限に太り続けないのはなぜだろうか ―― と考えたことはありませんか？

　「摂取カロリー＜基礎代謝カロリー+運動消費カロリー」が、減量の絶対方程式であるなら、 この不等式を、引っくり返せば「太り続ける」ことができるはずです。

　例えば、現在、体重66.5kgの私の基礎代謝カロリーは、1518kcal（キロカロリー）/日で、それに運動消費カロリー708kcal/日（歩行70分+電車60分+デスクワーク480分を週5日間として）を加えると2220kcal/日程度になります（このような計算をしてくれるサイトは、ネット上にたくさんあります）。

　ですから、その2220kcal/日を超える食事を取り続ければ、永久に太り続けることができるようにも思えます。

　実際、2220kcal/日を超える食事をすることは、簡単です。

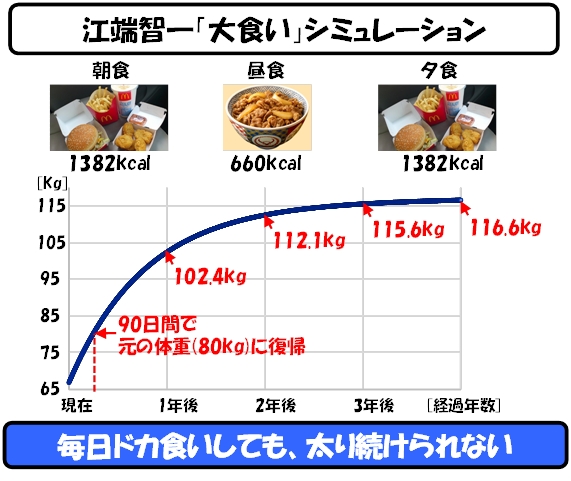
　私がマクドナルドで、ビッグマック、マックフライポテト（Mサイズ）、チキンマックナゲット（5個）、コーラ（Mサイズ）を頼むとすると、合計1382kcalですので、これを朝夕2食食べるだけでも、540kcal超過します。ここに吉野家の牛丼（並盛）660kcalを追加すれば、1140kcal/日超過です。

　さて、体重を1g増やすためには、7kcalのエネルギーが消費されずに体内に蓄積されれば足ります。ですから、上記のマクドナルドと吉野家で、私は1日163gの増量が可能です。このペースを続ければ、1年間に60kg太ることができ、16年後には、私の体重は1トンを超えるはずです。

　しかし、このようにはなりません。

　この食事（食事が違っても同じカロリー量であれば可）を、死ぬまで続けたとしても、私の体重は、絶対に118kgを超えることができないのです。

　なぜ、このような計算（シミュレーション）ができるかというと、「7kcal=1g」ということが、あらかじめ分っているからです。

　エネルギーがどこかに消えてなくなることがない（エネルギー保存法則）以上、「7kcalを余分に使えば1g痩せて、7kcalを余分に残せば1g太る」――。結局のところ、ダイエットとは、たったこれだけの単純な足し算と引き算のことなのです。